四面体OABCにおいて、![]() 、∠AOB = ∠BOC = ∠COA = 60° であるとする。また、辺OA上に点Pをとり、辺BC上に点Qをとる。以下、
、∠AOB = ∠BOC = ∠COA = 60° であるとする。また、辺OA上に点Pをとり、辺BC上に点Qをとる。以下、![]() とおく。
とおく。
(1) 0 ≦ s ≦ 1 , 0 ≦ t ≦ 1 であるような実数 s , t を用いて、
![]() と表す。
と表す。
![]() ア 、
ア 、 ![]() イ であることから
イ であることから
![]() = ( ウ s – エ )2 + ( オ t – カ )2 + キ
= ( ウ s – エ )2 + ( オ t – カ )2 + キ
となる。したがって、 ![]() が最小となるのは s = ク ケ , t = コ サ のときであり、このとき
が最小となるのは s = ク ケ , t = コ サ のときであり、このとき ![]() = √ シ となる。
= √ シ となる。
(2) 三角形ABCの重心をGとする。 ![]() = √ シ のとき、三角形GPQの面積を求めよう。
= √ シ のとき、三角形GPQの面積を求めよう。
![]() = ス から、∠APQ = セソ ° である。したがって、三角形APQの面積は √ タ である。また
= ス から、∠APQ = セソ ° である。したがって、三角形APQの面積は √ タ である。また
![]() = チ ツ
= チ ツ ![]() + テ ト
+ テ ト ![]()
であり、点 G は線分 AQ を ナ : 1 に内分する点である。
以上のことから、三角形GPQの面積は、 √ ニ ヌ である。
解答
アイ
まずは内積の定義通り、
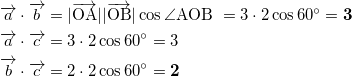
となる。
ウエオカキクケコサシ
問題で与えられた式を計算する。
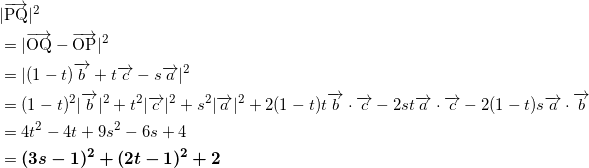
となるので、![]() が最小となるのは、
が最小となるのは、 ![]() のとき、
のとき、 ![]() である。
である。
※ここで、 ![]() であるから、Qは辺BCの中点であるということです。
であるから、Qは辺BCの中点であるということです。
![]()
を利用しています。センターのベクトルでよく出るんだ、これが。
スセソタ
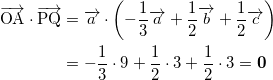
から、∠APQ = 90°である。
したがって、△APQは∠APQ = 90° の直角三角形ということだから、小学校で学んだ三角形の面積の公式で、
![]()
となる。
チツテトナ
![]() であるが、いま、
であるが、いま、
![]()
であることから、 ![]() である。よって、
である。よって、
![]()
となる。
この結果は、点Gは線分AQを 2 : 1 に内分する点であることを示している。(これは△ABCにおいて、重心は中線を 2 : 1 に分けるというよく知られた性質を示したことになる。)
ニヌ
よって、
![]()
となる。

コメント