第2問
解答
アイウエオカキ
まずは大体のグラフを書いて考えましょう(図は後で追加します。)
C1が上に、C2が下にあるので、求める面積Sは、
![Rendered by QuickLaTeX.com \begin{align*} S &= \int_a^{a+1} \left\{ \left( \frac{1}{2}x^2 + \frac{1}{2} \right) -\frac{1}{4}x^2 \right\} dx \\ &= \int_a^{a+1} \left( \frac{1}{\bm{4}}x^2 + \frac{1}{\bm{2}} \right) dx \\ &=\left[ \frac{1}{12}x^3 + \frac{1}{2}x \right]_a^{a+1} \\ &=\frac{1}{12} \{ (a+1)^3 -a^3 \} + \frac{1}{2} \{ (a+1) -a \} \\ &=\frac{1}{\bm{4}} a^2 + \frac{1}{\bm{4}} a + \bm{\frac{7}{12}} \end{align*}](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-42bd9780377a5acb73892de57167f77e_l3.png)
となる。これを平方完成すると、
![]()
となることから、![]() のとき、最小値
のとき、最小値 ![]() をとる。
をとる。
ソタチ
置いていかれないように、問題文をしっかり読んで、題意を把握します。
ただし、ソとタは問題文のところだけを読めば解けます。
y = 1 と C1 は、
![]()
を解いて、 x = ±1 で交わる。同様に、 y = 1 と C2 は、
![]()
を解いて、 x = ±2 で交わる。
このことから、 ![]() においては正方形Rと図形Dはまったく交わらなくなることがわかる。つまり、 0 ≦ a ≦ 2 のとき、RとDは空集合にならないといえる。
においては正方形Rと図形Dはまったく交わらなくなることがわかる。つまり、 0 ≦ a ≦ 2 のとき、RとDは空集合にならないといえる。
ツ
次に、1 ≦ a ≦ 2 のときを考える。正方形Rは C1 よりは完全に下で、かつ C2 によって一部切り取られている位置にある。よって、 a が増加するとき、Tは①減少する。
テト
0 ≦ a ≦ 1 のとき、図形Dのうち、正方形Rの外側にある部分の面積Uは、
![Rendered by QuickLaTeX.com \begin{align*} U &= \int_1^{a+1} \left\{ \left( \frac{1}{2}x^2 + \frac{1}{2} \right) -1 \right\} dx \\ &=\left[ \frac{1}{6}x^3 - \frac{1}{2}x \right]_1^{a+1} \\ &=\frac{1}{6}\{ (a+1)^3 -1 \} - \frac{1}{2} \\ &=\frac{1}{\bm{6}}a^3 + \frac{1}{\bm{2}}a^2 \end{align*}](http://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-1f2b64fd0f5aec28c4d2c51530b2089b_l3.png)
ナニヌ
求めるTは、T = S – U で与えられる。よって、
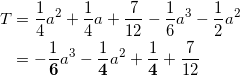
となる。
ネノハヒ
最後に、①の右辺を a で微分して増減を考える。
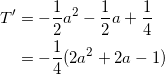
となる。ここで、 2a2 + 2a – 1 = 0 を解いて、![]() となるから、増減表は以下のとおり(省略)。
となるから、増減表は以下のとおり(省略)。
増減表より、Tは ![]() のとき最大値をとることがわかる。
のとき最大値をとることがわかる。

コメント