2014年センター数学IIB 第1問[2]

数学IIB講評　第1問[1]　第1問[2]　第2問　第3問　第4問　PDF　>>数学IA

第1問[2]

解答

ソタ

　log₂ 2³ = 3, log₃ 1 = 0であるから、
　　log₂ 2³ + log₃ 1² = 3 + 0 = 3
同様に、 log₂ 4³ = log₂ 2⁶ = 6, log₃ 3² = 2 であるから、
　　log₂ 4³ + log₃ 3² = 6 + 2 = 9
である。

チツテ

与えられた式を変形して、

(a) 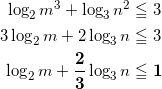$\begin{align*} \log_2 m^3 + \log_3 n^2 &\leqq 3 \\ 3 \log_2 m + 2 \log_3 n &\leqq 3 \\ \log_2 m + \bm{\frac{2}{3}} \log_3 n &\leqq \bm{1} \end{align*}$

となる。

トナニ

　n が自然数のとき、 log3 n のとり得る最小の値は 0 であるから、(a)式より、 log2 m ≦ 1 でなければならない。
　この条件を満たす自然数 m は m = 1 , 2 のいずれかである。

ヌネノハヒ

　m = 1 のとき、log2 1 = 0 であるから、(a)式に代入して、

$\begin{align*} \frac{2}{3} \log_3 n &\leqq 1 \\ \log_3 n &\leqq \bm{\frac{3}{2}} \end{align*}$

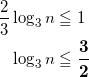
である。これを解くと、

$\begin{align*} \log_3 n &\leqq \frac{3}{2} = \log_3 3^{\frac{3}{2}} \\ n &\leqq 3^{\frac{3}{2}} = \sqrt{27} \\ n^2 &\leqq \bm{27} \end{align*}$

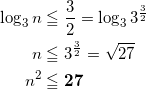
となる。よって、自然数 n の範囲は、n ≦ 5 である。
　以上より、 m = 1 のとき(a)式を満たす m , n のペアは 5 通りである。

フ

　同様に、 m = 2 のときは(a)式に log2 2 = 1 を代入して log3 n = 0 すなわち、
　　　n = 1
である。よって、 m = 2 のとき(a)式を満たす m , n のペアは 1 通りである。

ヘ

　以上より、(a)式を満たす m , n のペアは 5 + 1 = 6 通りである。