第3問
解答
アイウエオカキクケコ
階差数列が { bn } の数列{ an } の一般項は、
これを利用して解く。階差数列の第 n 項は 4n + 5 であるから、
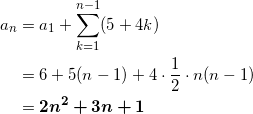
である(これは n = 1 のときも成立)。
最後に、
a2 = 8 + 6 + 1 = 15, a3 = 18 + 9 + 1 = 28
サシス
与えられた式?に n = 1 を代入して、
![]()
となる。
セソタ
?で n を n + 1 に置き換えた式は、
an+1 = 2 ( n + 1 )2 + 3 ( n + 1 ) + 1
であるから、これと?を?に代入して、
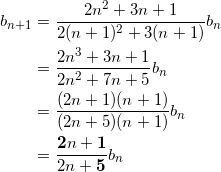
である。
チツ
問題文にあるように、
cn = ( 2n + 1 ) bn
とおくと、![]() を?式に代入して、
を?式に代入して、
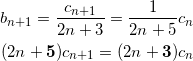
である。
テ
?の右辺 ( 2n + 3 ) cn の n を n + 1 に置き換えたものはちょうど左辺となるということは、この
dn = ( 2n + 3 ) cn
は恒等数列(すべての n に対して dn+1 = dn が成り立つ)であることが分かる。
ト
いま、
d1 = ( 2・1 + 3 ) c1 = 5c1
c1 = ( 2・1 + 1 ) b1 = 3b1
であるから、順番に計算していくと、
![]()
ナニ
部分分数分解は分子=分母の差でうまくいく
問題文に与えられた式を部分分数することで、
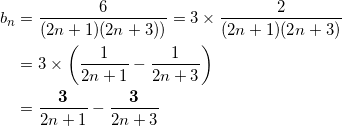
となる。
ヌネノ
この手の和は書き出したほうが見通しが良い。順に打ち消し合うことを利用して、
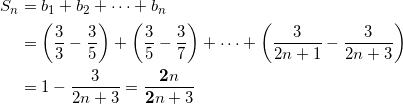
となる。

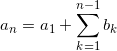
コメント