2020年センター数学IA 第2問[1]

2020年センター数学IA
　第1問[1]　第1問[2]　第1問[3]　第2問[1]　第2問[2]　第3問[1]　第3問[2]　第4問　第5問
　数学IA講評　PDF　>>数学IIB

　△ABCにおいて、BC = 2√2 とする。∠ACBの二等分線と辺ABの交点をDとし、CD = √2 , cos∠BCD = 34 とする。このとき、 BD = 　ア　であり
　sin∠ADC = √　イウ　　エ　
である。ACAD = √　オ　であるから
　　AD = 　カ　
である。また、△ABC の外接円の半径は　キ　√　ク　　ケ　である。

解答

ア

　△BCDにおいて余弦定理より、
　　BD² = BC² + DC² – 2・BC・DC cos∠BCD
　　　　　= 8 + 2 – 2×4×34 = 4
より、 BD = 2 （ > 0 ）

イウエ

　いま、
　　∠ADC = 180° – ∠BDC
であるから、
　　sin ∠ADC = sin ∠BDC
である。よって、sin ∠BDC を求めれば良い。

　△BCDにおいて正弦定理より、

$\frac{2\sqrt{2}}{\sin \angle \text{BDC}} = \frac{2}{\sin \angle \text{BCD}}$

であり、右辺分母について、

$\begin{align*} \sin \angle \text{BCD} &= \sqrt{ 1 - \cos \angle \text{BCD} } \\ &= \sqrt{1- \left( \frac{3}{4}\right)^2} \\ &= \frac{\sqrt{7}}{4} \end{align*}$

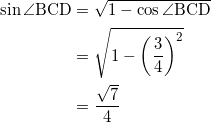
（sin∠BCD > 0）であるから、これを代入すると、
　　sin∠BDC = √144

オ

　角の二等分線の性質より、
　　AC : CB = AD : BD
すなわち
　　AC : AD = CB : BD = 2√2 : 2
であるから、
ACAD = √21 = √2
である。

カ

　ここで、 AD = k とおくと、AC = $\sqrt{2}k$ となるので、△ADCに余弦定理を用いて、
　　AD² = AC² + DC² – 2AC・DC cos∠ACD
　　k² = ( $\sqrt{2}k$ )² + 2 – 2× $\sqrt{2}k$ × $\sqrt{2}$ ×34
を整理すると、
　　k² – 3k + 2 = 0
　　( k – 1 ) ( k – 2 ) = 0
より k = 1 , 2 である。

　いま、 k = 2 のとき△ADCが成立しない（最長辺 AC が残りの2辺の和より大きくなる）ため k = 1 、すなわち、
　　AD = k = 1
である。

キクケ

　△ACDに正弦定理を用いて、
　　DCsin∠CAD = ADsin∠ACD
にそれぞれ数値を入れて、
　　sin∠CAD = √144
となる。

　次に、△ABCにおいて正弦定理により、△ABCの外接円の半径をRとすると、
　　BCsin∠A = 2R
が成り立つので、これをRについて解いて、
　　R = BC × 1sin∠A
　　　= 2√2 × 4√14
　　　= 4√77
となる。