△ABCにおいて、![]() 、
、 ![]() 、∠ABC = 60° とする。
、∠ABC = 60° とする。
(1) AC = √ ア であるから、△ABCの外接円の半径は √ イ であり
sin ∠BAC = √ ウ + √ エ オ
である。ただし、 ウ 、 エ の解答の順序は問わない。
(2) 辺AC上に点Dを、△ABDの面積が ![]() になるようにとるとき
になるようにとるとき
AB・AD = カ √ キ – ク ケ
であるから、 AD = コ サ である。
解答
ア
2辺と挟む角が分かっていれば、余弦定理
余弦定理より、
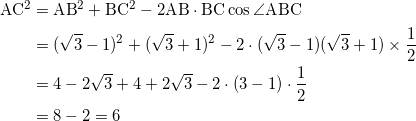
より、 ![]() 。
。
イ
外接円の半径は、正弦定理
求める外接円の半径を R とすると、正弦定理より、
![]()
が成り立つ。よって、
![]()
となる。
ウエオ
同じく正弦定理より、
![]()
が成り立つので、
![]()
となる。
カキクケ
三角形の面積の公式より、
![]()
より、
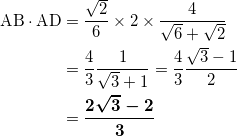
コサ
![]()
となる。

コメント