x は正の実数で、 ![]() を満たすとする。このとき
を満たすとする。このとき
![]() = アイ
= アイ
であるから、 ![]() = √ アイ である。さらに
= √ アイ である。さらに
x3 + 8x3 = ( x + 2x ) ( x2 + 4x2 – ウ )
= エ √ オカ
である。また
![]() = キク
= キク
である。
解答
アイ
実際に展開すると、
![]()
である。
ウエオカ
公式
![]()
において、![]() とおいて考えると、
とおいて考えると、
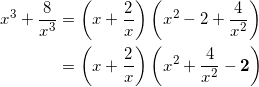
となり、ここに ![]() を代入して、
を代入して、
![]()
となる。
キク
■アイと同様の考え方で、ここでは ![]() をくくりだすように式変形して、
をくくりだすように式変形して、
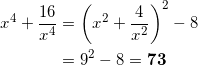
となる。

コメント