円周上に15個の点P0, P1, …, P14 が反時計回りに順に並んでいる。最初、点P0 に石がある。さいころを投げて偶数の目が出たら石を反時計回りに5個先の点に移動させ、奇数の目が出たら石を時計回りに3個先の点に移動させる。この操作を繰り返す。
例えば、石が点P5 にある時さいころを投げて6の目が出たら石を点P10に移動させる。次に、5の目が出たら、点P10にある石を点P7に移動させる。
(1) さいころを5回投げて、偶数の目が ア 回、奇数の目が イ 回でれば、点P0にある石を点P1に移動させることができる。このとき、 x = ア , y = イ は、不定方程式 5x – 3y = 1 の整数会になっている。
(2) 不定方程式
5x – 3y = 8 …①
のすべての整数解 x, y は K を整数として
x = ア ✕ 8 + ウ k , y = イ ✕ 8 + エ k
と表される。①の整数解 x, y の中で、 0 ≦ y < エ を満たすものは
x = オ , y = カ
である。したがって、さいころを キ 回投げて、偶数の目が オ 回、奇数の目が カ 回出れば、点P0にある石を点P8に移動させることができる。
(3) (2)においてサイコロを キ 回より少ない回数だけ投げて、点P0にある石を点P8に移動させることはできないだろうか。
(*)石を反時計回りまたは時計回りに15個先の点に移動させると元の点に戻る。
(*)に注意すると、偶数の目が ク 回、奇数の目が ケ 回出れば、さいころを投げる回数が コ 回で、点P0にある石を点P8に移動させることができる。このとき コ < キ である。
(4) 点P1, P2, …, P14のうちから点を一つ選び、点P0にある石をさいころを何回か投げてその点に移動させる。そのために必要となる、さいころを投げる最小回数を考える。例えば、さいころを1回だけ投げて点P0にある石を点P2へ移動させることはできないが さいころを2回投げて偶数の目と奇数の目が1回ずつ出れば、点P0にある石を点P2へ移動させることができる。したがって、点P2を選んだ場合には、この最小回数は2回である。
点P1, P2, …, P14のうち、この最小回数が最も大きいのは点 サ であり、その最小回数は シ 回である。
サ の解答群
⓪ P10 ① P11 ② P12 ③ P13 ④ P14
解答
アイ
合計5回なので、書き出して探す。
偶数5回、奇数0回の場合は 5✕5 = 25 進むが、15で一周になるので 25 – 15 = 10 より、P10にいる。
偶数4回、奇数1回の場合は 5✕4 – 3✕1 = 17 進む。17 -15 = 2 より、到着点はP2。
偶数3回、奇数2回の場合は 5✕3 – 3✕2 = 9 進む。到着点はP9。
偶数2回、奇数3回の場合は 5✕2 – 3✕3 = 1 進む。到着点はP1。よって、偶数が2回、奇数が3回。
ウエ
誘導に乗るようにしましょう。
5x – 3y = 8
に対して、
x = 16 + ak
y = 24 + bk
を代入して、
80 + 5ak – 72 – 3bk = 8
k ( 5a – 3b ) = 0
となる。すべての k に対してこの式が成り立つ a , b は a = 3, b = 5 である。
よって、
x = 2✕8 + 3k
y = 3✕8 + 5k
5・1 – 3 ・( -1 ) = 8
を不定方程式①から辺々引いて、
5(x-1) -3(y+1) = 0
とし、ここで5と3は互いに素なので、
x – 1 = 3k , y + 1 = 5k
とおいて、
x = 3k + 1 , y = 5k – 1
としてもよい。はじめに見つける特殊解によって、最後の項の数字が変わってくる。
オカキ
0 ≦ y < 5 を満たすのは、
y = 24 + 5k
より、 k = -4 のとき y = 4 。このとき x = 4 である。
偶数の目が4回、奇数の目が4回出ているので、サイコロは8回投げている。
クケコ
サシ
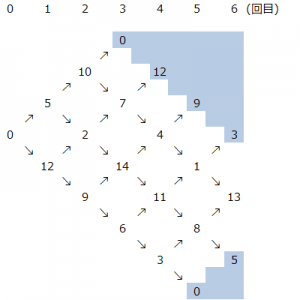
↗が偶数、↘が奇数を表すとき、さいころを投げるたびに次のように点を移動することが分かる。
以下の図から、最小回数が最も大きいのは点 ③ P13 で、その最小回数は6回である。

コメント