第1問[1]
解答
アイウエオ
( x + y ) ( x – y ) = x2 – y2 の公式を利用して、
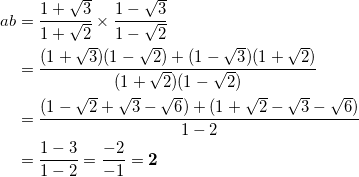
であり、
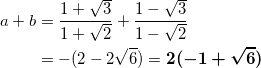
である。
カキク
( a + b )2 = a2 + 2ab + b2 より、
a2 + b2 = ( a + b )2 – 2ab
であるから、
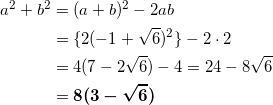
ケコ
素直に計算すればよく、
![]()
サシスセソ
いま、与えられた式より明らかに a ≠ 0 であるから、ab = 2 から ![]() が成り立つ。これを、今求めた
が成り立つ。これを、今求めた
a2 + b2 + 4 ( a + b ) = 16
に代入して、
![]()
となり、両辺に a2 を掛けて整理すると、
![]()
となる。

コメント