2016年センター数学IA 第3問

2016年センター数学IA
　第1問[1]　第1問[2]　第1問[3]　第2問[1]　第2問[2][3]　第3問　第4問　第5問
　数学IA講評　PDF　>>数学IIB

　赤球4個、青球3個、白球5個、合計12個の球がある。これら12個の球を袋の中に入れ、この袋からAさんがまず1個取り出し、その球をもとに戻さずに続いてBさんが1個取り出す。

(1)　AさんとBさんが取り出した2個の球の中に、赤球か青球が少なくとも1個含まれている確率は　アイ　　ウエ　である。

(2)　Aさんが赤球を取り出し、かつBさんが白球を取り出す確率は　オ　　カキ　である。これより、Aさんが取り出した球が赤球であったとき、Bさんが取り出した球が白球である条件付き確率は　ク　　ケコ　である。

(3)　Aさんは1球取り出したのち、その色を見ずにポケットの中にしまった。Bさんが取り出した球が白球であることがわかったとき、Aさんが取り出した球も白玉であった条件付き確率を求めたい。

　Aさんが赤球を取り出し、かつBさんが白球を取り出す確率は　オ　　カキ　であり、Aさんが青球を取り出し、かつBさんが白球を取り出す確率は　サ　　シス　である。同様に、Aさんが白球を取り出し、かつBさんが白球を取り出す確率を求めることができ、これらの事象は互いには違反であるから、Bさんが白球を取り出す確率は　セ　　ソタ　である。
　よって、求める条件付き確率は　チ　　ツテ　である。

解答

アイウエ

　「少なくとも」⇒余事象を考える。

　赤球も青球も含まれないというのは、すなわち白球しか取り出さないということ。AさんもBさんも白球を取り出す確率は、
　　 $\dfrac{5}{12} \times \dfrac{4}{11} = \dfrac{5}{33}$
よって、求める確率は、
　　 $\displaystyle 1 - \dfrac{5}{33} = \bm{\frac{28}{33}}$
である。

オカキ

　Aさんが赤球、Bさんが白球を取り出す確率は、
　　 $\displaystyle \frac{4}{12} \times \frac{5}{11} = \bm{\frac{5}{33}}$
である。

クケコ

　Aさんが赤球を取り出したときに、Bさんが白球を取り出す確率は、Bさんから見れば、11個の球から5個ある白球を引くことになるから、 $\displaystyle \bm{\frac{5}{11}}$ である。

問題の意味を考えれば、「条件付き確率」といわれても構える必要はありません。Aさんが“青球”を取り出したときの、Bさんが白球を取り出す確率も、同じく $\displaystyle \frac{5}{11}$ になります。

サシス

　Aさんが青球を取り出し、Bさんが白球を取り出す確率は、
　　 $\displaystyle \frac{3}{12} \times \frac{5}{11} = \bm{\frac{5}{44}}$
である。

セソタ

　どちらも白を取る確率は冒頭に求めた $\dfrac{5}{33}$ である。
　Aさんが赤球、Bさんが白球と取る確率は $\dfrac{5}{33}$ である。
　Aさんが青球、Bさんが白球と取る確率は $\dfrac{5}{44}$ である。
　これらは排反であるから、Bさんが白球を取る確率は、

$\begin{align*} \frac{5}{33} + \frac{5}{33} + \frac{5}{44} &= \frac{5}{11} \left( \frac{1}{3} + \frac{1}{4} + \frac{1}{3} \right) \\ &=\frac{5}{11} \times \frac{4+3+4}{12} = \bm{\frac{5}{12}} \end{align*}$

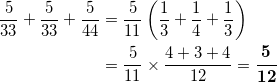
である。

チツテ

　Bさんが白球を取り出した時に、Aさんも白球を引いていたという条件付き確率は、
　「Bさんが白球を引く、という確率」分の「AさんもBさんも白球を引いていた、という確率」で求められるので、
　　 $\displaystyle \frac{\frac{5}{33}}{\frac{5}{12}} = \frac{12}{33} = \bm{\frac{4}{11}}$
である。