2015年センター数学IA 第2問[2]

数学IA講評　第1問　第2問[1]　第2問[2]　第3問　第4問　第5問　第6問　PDF版

第2問[2]

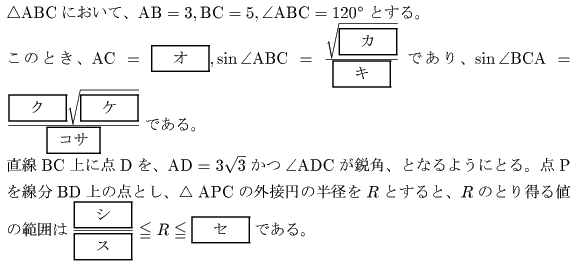
$15_1a_2_2$

解答

オカキクケコサ

　余弦定理より、

$\begin{align*} \text{AC}^2 &= \text{AB}^2 + \text{BC}^2 - 2 \text{AB}^2 \cdot \text{BC} \cos \angle \text{ABC} \\ &=34 + 15 = 49 \end{align*}$

より、AC = 7。
　また、暗記している角度であるから、 $\displaystyle \sin \angle \text{ABC} = \sin 120^{\circ} = \bm{\frac{\sqrt{3}}{2}}$ である。
　最後に、まず正弦定理より、

$\frac{\text{AC}}{\sin \angle \text{ABC}} = \frac{\text{BA}}{\sin \angle \text{BCA}}$

が成り立つので、これを解いて、

$\begin{align*} \sin \angle \text{BCA} &= \frac{\sin \angle \text{ABC}}{\text{AC}} \times \text{BA} \\ &= \frac{\sqrt{3}}{2} \times \frac{1}{7} \times 3 \\ &= \bm{\frac{3\sqrt{3}}{14}} \end{align*}$

である。

シスセ

　外接円の半径 R は、正弦定理より、

$R = \frac{\text{AP}}{2\sin \angle \text{BCA}} = \frac{7}{3\sqrt{3}} \text{AP}$

で与えられる。
　今、A, B, C, D, P の位置関係は図は以下の通りで（図は後日挿入）、線分APの長さは、点PがBからDまで動く間に様々な値を取る。

　APが最小となるのは、点PがAから線分BD上への垂線の足の位置であるときで、そのときのAPの長さは、 $\displaystyle \text{AP} = \frac{3\sqrt{3}}{2}$ である。よって、Rの最小値は、

$R_{min} = \frac{7}{3\sqrt{3}} \times \frac{3\sqrt{3}}{2} = \bm{\frac{7}{2}}$

である。
　次に、APが最大となるのは、PがDと一致するときで、 $\text{AP} = 3\sqrt{3}$ である。よって R の最大値は、

$R_{max} = \frac{7}{3\sqrt{3}} \times 3\sqrt{3} = \bm{7}$

である。