大学入試数学演習 大学入試数学演習
大学入試数学演習 
大学入試数学演習 複素数平面と鋭角三角形 ［2016 東京大・理］
大学入試数学演習 有理数・無理数の稠密性 ［2016 大阪大・専門数学］
大学入試数学演習 垂線の足が対面の外心である四面体 ［2016 京都大・理］
大学入試数学演習 n進法で表される等式 ［2016 京都大・文］
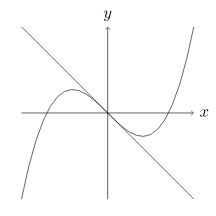
大学入試数学演習 3次関数と接線の本数 ［2016 早稲田大・理工］
大学入試数学演習 巡回群の直積と位数 ［2016 慶應大・理工］
大学入試数学演習 約数の個数と和 ［2016 慶應大・理工］
大学入試数学演習 数学的帰納法 ［1998 早稲田大・政経］
大学入試数学演習