3の倍数と3のつく数でアホになるとき、10000まで数える間にアホにならない回数は？【テレビ番組】

問題

『3の倍数と3のつく数の時にアホになる』というネタが流行したことがあった。
さて、1以上10000以下の整数のうちアホにならないものは全部でいくつあるか。
　

番組：2015年12月30日24時10分～「IQヴィーナス」テレビ東京より
http://www.tv-tokyo.co.jp/iqvenus/

イズミの解答への道

　適度に頭を使うよい問題です。受験を前に、こういうパズル的な問題で頭を柔らかくしておくのもよいでしょう。
　「3の倍数と3の付く数」を数えるのは大変なので、その逆を行くほうが効率的だと予想します。

解答

　3がつかず、かつ3の倍数でもない数字の数を考える。
　
　まず、3が付かない数は、0,1,2,4,5,…,9 から重複を含んで無作為に選ぶ4桁の数であるから、 9⁴ 個ある。ただしここには、0000、すなわち0も含む。
　つぎに、これらのうち3の倍数になってしまう数を除く。3の倍数とは、「各桁の和が3の倍数になるもの」である。
　まず、4桁のうち3桁を（3を除く9個の数字から）適当に選ぶ。（例：174*）
　次に、すでに選んだ数字の合計が、

3の倍数になっている場合は、残りの1桁は 0,6,9 のいずれか
3で割ってあまり1となる場合は、残りの1桁は 2,5,8 のいずれか
3で割ってあまり2となる場合は、残りの1桁は 1,4,7 のいずれか

であればよく、これらは同時には起こり得ないが、いずれの場合も最後の桁は3つの数から選ぶこととなる。
　例えば、はじめに 174* とした場合、この3桁の和は 1 + 7 + 4 = 12 なので、残りの桁は 0 , 6 , 9 のいずれかであればよい。
　よって、3を除いて作った数のうち、3の倍数は 9 × 9 × 9 × 3 個である。

　以上より、3を含まない 0から9999までの数（9⁴個）のうち、3の倍数は 9³ ×3 個あるので、求める個数は、
　　9⁴ – 9³ × 3 = 4374個
である。

　最後に、

この計算上、0は3の倍数として、カウントからすでに除外されていること、
10000は題意を満たす数である

ことから、
　　4374 + 1 = 4375個
が正解。

解説

その他に出題された問題と解答

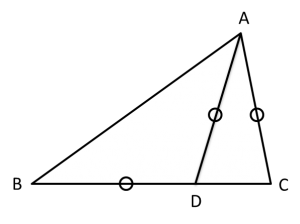
△ABCの辺BC上に点Dをとる。∠ABD = 40°、AC = AD = BD のとき、∠CAD = ？
$Picture1$

【解答】
　中学校の問題です。∠ABD = ∠BAD = 40°だから、
　　∠ADC = ∠ABD + ∠BAD = 80°
となる。△ADCも二等辺三角形なので、∠ADC = ∠ACD = 80°だから、
　　∠CAD = 180° – ( 80° + 80° ) = 20°

$\sqrt{676}$ 　ルートを外すといくつ？

【解答】
　26² = 676 より、 26 、では味気が無いので、素早い考え方を考えましょう。

　まず、明らかに $20 < \sqrt{676} < 30$ です。
　次に、早押し問題ですから、整数になるのでは、という想定をします。
　整数だとすれば、2乗して下一桁が6になる数ということから、一桁目は4か6かな、と想定します。つまり答えは24か26の可能性が高い。
　算数が少し得意であれば、 25² = 625 ぐらいは覚えていてもいいでしょう。そうすると答えは25よりも大きい数字だから、26になるかな、と予想します。
　さて、26の2乗の暗算は、
　　( 25 + 1 )² = 625 + 50 + 1 = 676
と計算できますね。
　以上を5秒ぐらいでやれれば、普通の算数好きとしては合格でしょう。

簡単にせよ。
$\log_2 1 + \log_2 2 + \log_2 3 + \log_2 4 + \log_2 6 + \log_2 9 + \log_2 {12} + \log_2 {18} + \log_2 {36}$

【解答】
　これはまじめに計算するしかないです。
　式で書けば下の通りですが、結局は掛け合わせたときに、2の指数がいくつか、3の指数がいくつか、というところだけに着目すればよいということです。

$\begin{align*} &\log_2 1 + \log_2 2 + \log_2 3 + \log_2 4 + \log_2 6 + \log_2 9 + \log_2 {12} + \log_2 {18} + \log_2 {36} \\ &=\log_2 (1 \cdot 2 \cdot 3 \cdot 4 \cdot 6 \cdot 9 \cdot 12 \cdot 18 \cdot 36 ) \\ &=\log_2 (2^{1 + 2 + 1 + 2 + 1 + 2} \cdot 3^{1+1+2+1+2+2}) \\ &=\log_2 2^9 + \log_2 3^9 = \bm{9 + 9 {\log_2} 3} \end{align*}$

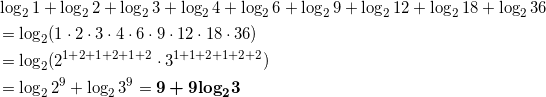
次の問題に答えなさい。
次の図のマス目に数字を入れて、縦、横、斜め一列の和が全て等しくなるようにしたい。？に当てはまる数を答えよ。

$\begin{array}{|c|c|c|} \hline & & 48 \\ \hline 27 & & \\ \hline 34 & ? & \\ \hline \end{array}$

【解答】
　左上のマスに入る数を a とおく。中央の数字を b とおくと、
　　a + 27 + 34 = 34 + b + 48
より、 b = a – 21 となる。

$\begin{array}{|c|c|c|} \hline a & & 48 \\ \hline 27 & a-21 & \\ \hline 34 & ? & \\ \hline \end{array}$

　この時点で、一列の合計は、 a + 61 になることに気付くとあとの計算が早い。
　中央行（ヨコ）について、合計が a + 61 になるということは、中央右端は、
　　( a + 61 ) – { 27 + ( a – 21 ) } = 55
であり、右端の列についても、合計が a + 61 になることから、右下は、
　　( a + 61 ) – ( 48 + 55 ) = a – 42
であることが分かる。

$\begin{array}{|c|c|c|} \hline a & & 48 \\ \hline 27 & a-21 & 55 \\ \hline 34 & ? & a-42 \\ \hline \end{array}$

　最後に、一番下の行について、合計が a + 61 になることから、求めるマスの値を x とおけば、
　　34 + x + ( a -42 ) = a + 61
より、 x = 69 と求められる。答えは 69 。

これも、チェバの定理を知っていれば一瞬です。

1から1000までの奇数をすべて足すといくつ？

【解答】
　これは、数学Bで学ぶ等差数列の和の公式さえ分かっていれば暗算でできる問題です。
　初項は1、最後の項は999、項の数は500なので、

$( 1 + 999 ) \times 500 \times \frac{1}{2} = \bm{250000}$

で3秒で解ける問題なのですが、番組では誤答が連発でした。緊張していたのでしょうか。

3個のさいころを同時に振るとき出た目の和がちょうど7になる確率を求めよ。

【解答】
　これは、普通の場合の数と確率の問題ですね。
　出る目が7となる目の組み合わせは (1,1,5) , (1,2,4) , (1,3,3) , (2,2,3) の4種類の並び替えしかない。
　それぞれの並び替えを考えると、(1,1,5)は $\displaystyle \frac{3!}{2!}=3$ より3通り、(1,2,4)は3!=6通り、(1,3,3)は3通り、(2,2,3)は3通りあるので、合計15通り。
　よって求める確率は、 $\displaystyle \frac{15}{216} = \bm{\frac{5}{72}}$ となる。

問題

イズミの解答への道

解答

解説

その他に出題された問題と解答

コメント