初耳学
2016年11月20日放送の「林先生も驚く!初耳学」という番組で、ベルヌーイ螺旋というものが紹介されていました。この記事では、ベルヌーイ螺旋について少し詳しく解説していきます。
まずは、番組で紹介された内容を紹介します。
従来のハサミは、ダンボールのような厚手のものを切るときに、根本では切れるけど、先端では切れない、ということがあります。しかし、最新のハサミにはどこで切っても同じ切れ味の(先端でも厚手のものが切れる)ハサミがある。さて、なぜどこでも同じ切れ味なのか?
このような問題に対して、林先生が自らの知識で説明していくところが見られたり、あるいは説明できないちょっと格好悪い林先生を見られるところが、この番組の見どころですね。
さて、この問題の答えは次のとおりです。
ハサミの切れやすさは2枚の刃の為す角度で決まり、従来のハサミは根本と先端で刃の為す角度が違っていた(根本は切れやすい角度、先端は切りにくい角度)。しかし先端のハサミでは、根本から先端まで刃の為す角度が一定になるように設計されているために、どこでも切りやすさが変わらない。
ちなみに、林先生は見事正解を出していました。そして、この「角度が一定」となる新しいハサミのは、実はベルヌーイ螺旋という考え方を利用して作られているということを林先生が紹介します。以下では、ベルヌーイ螺旋とは何者なのか、数学的に詳しく説明をシていきたいと思います。
ベルヌーイ螺旋とは
数学の世界では、特徴のあるさまざまな図形に名前をつけます。たとえば、ボールを投げたときに描く孤を放物線といいますが、これも数学の世界ではれっきとした図形の名前です。
ベルヌーイ螺旋も同じようなもので、番組でも説明されていましたが、アンモナイトのうずまきや、台風(低気圧)の雲の形がベルヌーイ螺旋と呼ばれる形状になっていることが知られています。
また、ベルヌーイ螺旋の特徴として、
- この螺旋状のどの点をとっても、その点と原点を通る直線と、その点における接線が交わる角度が一定になる
数学的な説明
ここから先は、数学の知識をフル活用したベルヌーイ螺旋の説明です。
まずは定義を紹介します。ベルヌーイ螺旋とは、
x = aebθ cos θ
y = aebθ sin θ
で定義される図形で、極座標表示に直せば、
r = aebθ
とも表示することができます。
この定義をもとに、冒頭で紹介した、「この螺旋状のどの点をとっても、その点と原点を通る直線と、その点における接線が交わる角度が一定になる」という性質を証明してみましょう。
基本的にはベクトルを利用して証明します。ベルヌーイ螺旋状のある点P ( aebθ cos θ , aebθ sin θ ) をとります。その点と原点を通る直線とは![]() となります。
となります。
次に、この点における接線の向きは、それぞれの成分をθで微分した、
( aebθ(b cos θ – sin θ ) , aebθ(b sin θ + cos θ ) )
となります1ので、あとは、このベクトルと![]() のなす角 X が一定であることを示せばよいのです。ここは高校数学を利用して、 cos X の値がθによらないことを示します。
のなす角 X が一定であることを示せばよいのです。ここは高校数学を利用して、 cos X の値がθによらないことを示します。
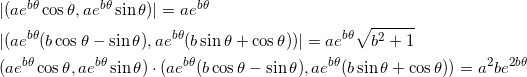
であるから、
![]()
となり、角 X はパラメータθによらないことが示された。
この証明とまったく同じ問題が、2000年の神戸大学の入試問題にあるので、高校生の人はこちらをみてください。

また、ベルヌーイ螺旋は、その弧長を容易に計算できる(基本的な積分で求めることが出来る)ことが有名です。実際以下のような大学入試問題が出題されています。

コメント