第4問
解答
アイウ
すべての辺の長さが 1 で、∠AOC = 120°のようなひし形を考えると、
∠AOB = 60°, OB = 1(すなわち、△OAB、△BOCは辺の長さが 1 の正三角形)
である。
点Pは線分 AB を 2 : 1 に内分する点であるから、
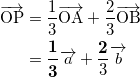
である。
エ
いま、
![]()
だから、
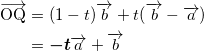
である。
オカキ
いま、
![]()
であり、OPとOQは直角に交わることより
![]()
である。
クケ
いま、
![]()
であり、OPとOQは直角に交わることより
![]()
である。
![]() より、
より、
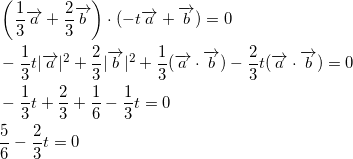
をといて、![]() である。
である。
コサシスセソタチツ
いま、
![]()
より、![]() であり、
であり、
![]()
より、![]() である。
である。
これらより求める面積は、
![]()
である。
テトナニ
誘導に乗って、問題文に与えられた通り、
![]()
にそれぞれ代入すると、
![]()
となる。ここで、![]() と
と![]() は一次独立だから、
は一次独立だから、![]() の係数、
の係数、![]() の係数がそれぞれ等しくならなければならないので、
の係数がそれぞれ等しくならなければならないので、
![Rendered by QuickLaTeX.com \[ \begin{cases} -\frac{1}{4} r = \frac{1}{3} (1-s) - \frac{5}{4}s \\ r = \frac{2}{3} (1-s) + s \end{cases} \]](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-bd9e52028758728e1e372ff720f257ce_l3.png)
を解いて、
![]()
となる。
ヌネノハヒフ
今得られた r , s を代入して、
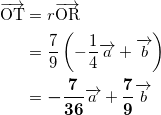
である。
ヘホ
最後に、r, s の値から、 OT : TR = 7 : 2 , PT : TQ = 1 : 2 であることから、
△PTO : △PRT = 7 : 2,
△PTO : △QTO = 1 : 2
であるから、
△PQO : △PRT = 7×(1+2) : 2 = 21 : 2
である。

コメント