解と係数の関係を学ぶ前に
はじめに例題から見てみよう。
2次方程式 x2 – 5x + 3 = 0 の2つの解の和はいくつか。また積はいくつか。
解答?
中学生でも解けそうな問題です。やってみましょう。2つの解を、![]() とおくと、
とおくと、
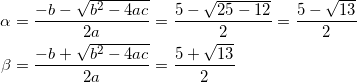
となるので、和は、
![]()
であり、積は、
![]()
となる。
ちょっと面倒くさいですが、難しいところはないようです。しかし、今回のテーマである「解と係数の関係」という必殺技を使うと、この問題をいともかんたんに解くことができるのです。その必殺技を学んでいきましょう。
解と係数の関係
さっそく、教科書にある「解と係数の関係」を見てみましょう。
【解と係数の関係】
2次方程式 ax2 + bx + c = 0 の解をとすると、
である。
教科書には上のように書いてありますが、これだけでは「だから?」となってしまって、どこがポイントなのかわかりづらいですね。
ここで言っていることは、「2次方程式の2つの解について、その“和”と“積”であれば、2次方程式を解かなくても、もと2次方程式(の係数)を見ればすぐ分かるよ!」ということなのです。
そのような見方をして、上の例題を「解と係数の関係」を使って解いてみよう。
2次方程式 x2 – 5x + 3 = 0 の2つの解の和はいくつか。また積はいくつか。
解答
和は係数 a と b を使います。分子が1次の係数 b 、分母が2次の係数 a 、そしてマイナスを付けます。
x2 – 5x + 3 = 0
の下線部。いま、2次の係数 a = 1 であるから割ることは考えなくて良いので、
和 = – (1次の係数) = – (-5) = 5
となります。
積は係数 a と定数項 c を使います。分子が定数項 c 、分母が2次の係数 a 。先ほどと違ってマイナスは不要です。定数項は、
x2 – 5x + 3 = 0
の下線部。同じく2次の係数 a = 1 だから、
積 = (定数項) = 3
となります。
冒頭では解の公式を使って解を求め、ルートが入った計算をして求めましたが、解と係数の関係を使うと簡単に求めることができました。これが解と係数の関係を使うメリットです。
ちょっと練習してみよう
例題で少し練習してみよう。
次の2次方程式の2つの解を α , β とするとき、和 α + β と積 αβ を求めよ。
(1) x2 – 6x + 5 = 0 (2) x2 – 2x – 4 = 0
(3) 3x2 – 5x – 9 = 0 (4) 2x2 + 9x + 1 = 0
解答
それぞれ、解と係数の関係より、
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
学生の方なら、手持ちの参考書に必ず問題が載っているはずなので、同じ問題を探して問いてみて欲しい。
解と係数の関係は対称式と相性がいい
実は解と係数の関係の問題は、次のような問題で出ることが多い。上の例題でみたような、和 α + β や積 αβ を求めるだけでは簡単すぎるのである。
2次方程式 x2 – 5x + 3 = 0 の解を α , β とするとき、次の値を求めよ。
(1) α + β (2) α2 + β2
(3) α3 + β3 (4) 1α + 1β
この問題を解くコツは、対称式の扱いにある。解と係数の関係では、和 α + β や積 αβ の値しか求めることはできないので、与えられたα2 + β2 のような式を、なんとか α + β や αβ で表すことを考えなければならない。これも高校数学必須の技法で「対称式」と呼ばれるものであり、次のページで先に学んでおいてもらいたい。
解答
まずは、解と係数の関係より、
α + β = 5 , αβ = 3
である。
(1) α + β = 5
(2) α2 + β2
= ( α + β )2 – 2αβ
= 25 – 6 = 19
(3) α3 + β3
= ( α + β )3 – 3αβ ( α + β )
= 125 – 3・3・5 = 80
(4) 1α + 1β
= α + βαβ = 53

コメント