定積分 ![]() を求めよ。
を求めよ。
[2007 京都大・理乙]
イズミの解答への道
積分はある程度は慣れですが、「なんとなく」で解いているようでは答えにたどり着くのに時間がかかってしまいます。基本的なテクニックをしっかり身に着けていれば、「ピンポイント置き換え」型に当てはめつつ、うまくいかない部分は x = a tanθ と置き換えられそうなパターンだ、と見ぬくことができるでしょう。
解答
![]()
と分けて考える。
(前半)
![]() とおくと、
とおくと、 ![]() であり、
であり、 ![]() のとき
のとき ![]() だから、
だから、
![Rendered by QuickLaTeX.com \begin{align*} \int_0^2 \frac{2x}{\sqrt{x^2+4}} dx &= \int_4^8 \frac{1}{\sqrt{t}} dt \\ &=[ 2 \sqrt{t} ]_4^8 = 4 \sqrt{2} - 4 \end{align*}](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-a0ac8f642d8473a6a8b5928afc2af376_l3.png)
となる。
(後半)
![]() とおくと、
とおくと、 ![]() であり、
であり、 ![]() のとき、
のとき、 ![]() であるから、
であるから、
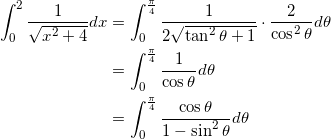
さらにここで ![]() とおくと、
とおくと、![]() であり、
であり、 ![]() は
は ![]() となるから、
となるから、
![Rendered by QuickLaTeX.com \begin{align*} \int_0^2 \frac{1}{\sqrt{x^2+4}} dx &= \int_0^{\frac{1}{\sqrt{2}}} \frac{1}{1-t^2} \\ &=\int_0^{\frac{1}{\sqrt{2}}} \frac{1}{2} \left( \frac{1}{1-t} + \frac{1}{1+t} \right) dt \\ &=\frac{1}{2} \left[ \log \left| \frac{1+t}{1-t} \right| \right]_0^{\frac{1}{\sqrt{2}}} \\ &=\frac{1}{2} \log \frac{\sqrt{2}+1}{\sqrt{2}-1} \\ &=\frac{1}{2} \log ( \sqrt{2} + 1)^2 \\ &=\log (\sqrt{2}+1) \end{align*}](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-9cc4a27e2feee3f1194e1f3639c29441_l3.png)
以上より、
![]()
である。
解説
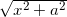 を含む積分
を含む積分
![]() が含まれる積分は、難しい積分のパターンの1つです。
が含まれる積分は、難しい積分のパターンの1つです。
とはいえ、 ![]() が分母にある場合は上述のように a = tanθ と置き換えれば解くことができます。
が分母にある場合は上述のように a = tanθ と置き換えれば解くことができます。
しかし、分子にある場合、つまり、
![]()
という積分は a = tanθ という置き換えでも解くことができません。
ところで、 ![]() を含む積分は、以下の方法で統一的に解くことができます。そこで、別解としてその解法を上げておきましょう。ポイントは、
を含む積分は、以下の方法で統一的に解くことができます。そこで、別解としてその解法を上げておきましょう。ポイントは、
![]()
とおくことです。脈略がないので「なぜ?」と思うかと思いますが、ここでは「 ![]() を含む積分は、このように置き換える」と覚えておくとよいでしょう。なぜこの解き方ができるかは別ページで紹介します。
を含む積分は、このように置き換える」と覚えておくとよいでしょう。なぜこの解き方ができるかは別ページで紹介します。
別解
![]() とおくと、
とおくと、
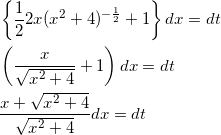
となり、 ![]() であったから、
であったから、
![]()
となる。また積分範囲は、
であるから、後半部分の積分は、
![Rendered by QuickLaTeX.com \begin{align*} \int_2^{2+2\sqrt{2}} \frac{1}{t} dt &= [\log t ]_2^{2+2\sqrt{2}} \\ &= \log(2+2\sqrt{2}) - \log 2 \\ &= \log (1+\sqrt{2}) \end{align*}](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-5e0d22802655182e6ceec4dcca199e2a_l3.png)
となる。

コメント