カルダノの公式で得られる整数解［2002 大阪教育大（後）］

　 $\displaystyle \alpha= \sqrt[3]{\sqrt{\frac{28}{27}}+1} - \sqrt[3]{\sqrt{\frac{28}{27}}-1}$ とする。
(1)　整数を係数とする3次方程式で、αを解に持つものがあることを示せ。
(2)　αは整数であることを示せ。また、その整数を答えよ。

［2002 大阪教育大（後）］

イズミの解答への道

　見た目のいかつい式であるが、これが実は整数である、ということを示す問題。設問に沿っていけば答えは得られる。(1)では3次方程式を求めるのだから、まずは3乗してみるしかありません。(2)はその3次方程式から得られる実数解がαしか存在しないことから証明されます。

解答

　　 $\displaystyle p = \sqrt[3]{\sqrt{\frac{28}{27}}+1} , \quad q =\sqrt[3]{\sqrt{\frac{28}{27}}-1}$
とおくと、
　　α³ = (p-q)³ = p³ – q³ -3pq (p-q)
であり、いま、
　　 $\displaystyle p^3 = \sqrt{\frac{28}{27}}+1 ,\quad q^3 =\sqrt{\frac{28}{27}}-1$
より、 p³ – q³ = 2 であり、

$\begin{align*} pq &= \sqrt[3]{ \left( \sqrt{\frac{28}{27}}+1 \right) \left( \sqrt{\frac{28}{27}}-1 \right) } \\ &= \sqrt[3]{\frac{28}{27} - 1} \\ &= \sqrt[3]{\frac{1}{27}} = \frac{1}{3} \end{align*}$

であることから、

$\begin{align*} \alpha^3 &= p^3 - q^3 - 3pq(p-q) \\ &= 2 - 3 \cdot \frac{1}{3} \alpha \\ &= 2 - \alpha \end{align}$

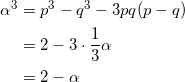
が成り立つ。これを整理して、求める方程式は α³ + α -2 = 0 である。

(2)　題意より、与えられた α は実数であり、方程式 x³ + x -2 = 0 の解である。いま、方程式 x³ + x -2 = 0 は、
　　( x – 1 ) ( x² + x + 2 ) = 0
と因数分解されるが、方程式
　　x² + x + 2 = 0
の判別式
　　D = 1 – 4・1・2 < 0 となることより、方程式 x² + x + 2 = 0 は実数解を持たない。
　以上より、与えられた実数 α は方程式 x³ + x -2 = 0 の解であると結論づけられる。このとき α = 1 である。

解説

カルダノの公式とは

　3次方程式を一般的に解く方法として、カルダノの公式というものがある。この片鱗に触れることのできる問題である。カルダノの公式について、実際に(1)で得た3次方程式を使って紹介していこう。

　まず、恒等式
　　( u + v )³ -3uv ( u + v ) – ( u³ + v³ ) = 0
について、 x = u + v とおく。
　(1)の方程式を考えるときには、
　　3uv = -1 , u³ + v³ = 2　　…(a)
を満たす u , v を見つけることができれば、その解は x = u + v と表すことができる。
　(a)より、

$u^3 v^3 = -\frac{1}{27} , \quad u^3+ v^3 = 2$