問題
f ( x ) = x3 – x とする。xy平面上の点 ( p , q ) から直線 y = f ( x ) へ引いた接線を考える。次の問に答えよ。
(1) 直線 y = m ( x – p ) + q が曲線 y = f ( x ) の接線となるための条件を m , q , p を用いて表わせ。
(2) 点 ( p , q ) から曲線 y = f ( x ) に3本の接線を引くことができるとき、 p , q の条件を求めよ。
(3) (2)の条件を満たす点 ( p , q ) の範囲を図示せよ。
イズミの解答への道
3次関数に引ける接線の本数の問題は、頻出問題。受験用の問題集を解いていれば、必ず一度は出会っているだろう。(1)の出題は異例だが、(1)ができなくとも(2)と(3)は必ず解けるようにしたい。
解答
(1) y = f ( x ) 上の接点を ( t , t3 – t ) とおくと、この接線は、
y = ( 3t2 – 1 ) ( x – t ) + t3 – t
= ( 3t2 – 1 ) x – 2t3
となる。これと y = m ( x – p ) + q を比較して、
m = 3t2 – 1 , -mp + q =2t3
となるので、t について解けば、
![]()
となるので、
4 ( m + 1 )3 = 27 ( mp – q )2
となる。
(2) y = f ( x ) 上の点 ( t , t3 – t ) を接点とする接線は、
y = ( 3t2 – 1 ) x – 2t3
であり、これが ( p , q ) を通るので、
q = ( 3t2 – 1 ) p – 2t3
を満たせば良い。そして接線が3つあるということは、接点が3か所、すなわちこれを t についての方程式と見たときに、異なる3つの解をもてば良い。
g ( t ) = 2t3 – 3pt2 + p + q
とおくと、
g’ ( t ) = 6t2 – 6pt
= 6t ( t – p )
となる。
いま、 y = g ( t ) と y = g ( 0 ) が3つの交点を持てばよく、そのためには、
![]() かつ
かつ ![]()
または ![]() かつ
かつ ![]()
であればよく、それは
p ≠ 0 かつ ![]()
ということである。これより求める条件は、
![]()
(3) 作成中
解説
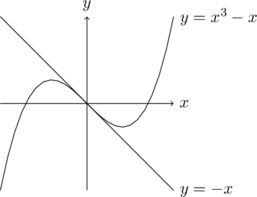
3次関数と接線の本数
3次関数の接線の本数に関する出題は頻出問題で、その解き方と同時に、結果も覚えておいてよいだろう。
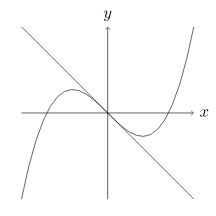
以下の図のように
コメント