シグマ公式の証明［2010 九州大・文］

　以下の問いに答えよ。答えだけでなく、必ず証明を示せ。
(1)　和 1 + 2 + … + n を n の多項式で表せ。
(2)　和 1² + 2² + … + n² を n の多項式で表せ。
(3)　和 1³ + 2³ + … + n³ を n の多項式で表せ。

［2010 九州大・文］

イズミの解答への道

　基本的な公式をきちんと証明できますか、という問題。教科書に載っているものの、(2)、(3)は巧妙なやり方ですから、知らないと難問です。
　解説では他の証明方法の紹介と、過去の入試で出題された関連する問題の紹介を行います。

解答

(1)　求める和を S とおくと、
　　　S = 1 + 2 + … + n
であり、これを逆順に並べた
　　　S = n + ( n – 1 ) + … + 1
も同じく S であるから、これらを足し合わせると、
　　　2S = ( n + 1 ) + ( n + 1 ) + … + ( n + 1 )
を整理して、

$S = \bm{\frac{1}{2}n(n+1)}$

(2)　k + 1 の3乗の公式
　　　( k + 1 )³ = k³ + 3k² + 3k + 1
を変形した、
　　　( k + 1 )³ – k³ = 3k² + 3k + 1
において、 k = 1 , 2 , … , n としたものを辺々足し合わせると、

$\begin{array}{clll} (k=1) \quad & 2^3 - 1^3 &= 3 \cdot 1^2 & + 3 \cdot 1 +1 \\ (k=2) \quad & 3^3 - 2^3 &= 3 \cdot 2^2 & + 3 \cdot 2 +1 \\ (k=3) \quad & 4^3 - 3^3 &= 3 \cdot 3^2 & + 3 \cdot 3 +1 \\ &\quad \vdots & \quad \vdots &\quad \vdots \\ (k=n) \quad & (n+1)^3 - n^3 &= 3 \cdot n^2 & + 3 \cdot n + 1 \\ \hline & (n+1)^3 - 1^3 &=\displaystyle 3 \sum_{k=1}^n k^2 &\displaystyle +3 \sum_{k=1}^n k + n \end{array}$

より、

$(n+1)^3 - 1^3 = 3 \sum_{k=1}^n k^2 +3 \sum_{k=1}^n k + n$

が成り立つ。(1)の結果を用いて整理すると、

$\begin{align*} 3 \sum_{k=1}^n k^2 &= (n+1)^3 - 1 - 3 \times \frac{1}{2}n(n+1) - n \\ &= n^3 + 3n^2 + 3n - \frac{3}{2}n^2 - \frac{3}{2} n - n \\ &= n^3 + \frac{3}{2}n^2 + \frac{1}{2} n \\ \sum_{k=1}^n k^2 &= \frac{1}{3} \cdot \frac{1}{2} ( 2n^3 + 3 n^2 + n ) \\ &= \frac{1}{6}n (2n^2 + 3n +1 ) \\ &= \bm{\frac{1}{6}n (n+1)(2n+1) } \end{align*}$

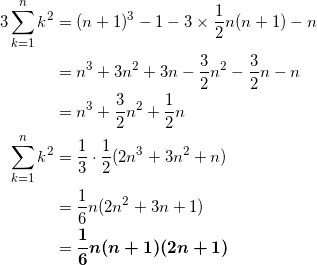
となる。

(3)　(2)と同様に、
　　( k + 1 )⁴ – k⁴ = 4k³ + 6k² + 4k + 1
を k = 1 から k = n まで書き下して辺々足すと、

$(n+1)^4 - 1^4 = 4\sum_{k=1}^n k^3 + 6 \sum_{k=1}^n k^2 + 4 \sum_{k=1}^n k + n$

となる。(1)、(2)の結果を用いて整理すると、

$\begin{align*} \sum_{k=1}^n k^3 &= \frac{1}{4} \biggl\{ (n+1)^4 -1^4 \\ & \qquad -6 \cdot \frac{1}{6}n(n+1)(2n+1) - 4 \cdot \frac{1}{2} n(n+1) -n \biggr\} \\ &=\frac{1}{4} \{ n^4 + 4n^3 + 6n^2 + 4n \\ &\qquad \qquad - n(n+1)(2n+1) - 2n(n+1) - n \} \\ &=\frac{1}{4}n ( n^3 + 4n^2 + 6n + 4 \\ &\qquad \qquad - (n+1)(2n+1) - 2(n+1) -1 ) \\ &=\frac{1}{4}n ( n^3 + 2n^2 + n ) \\ &=\frac{1}{4}n^2 ( n^2 + 2n + 1) \\ &= \bm{ \left\{ \frac{1}{2} n(n+1) \right\}^2} \end{align*}$

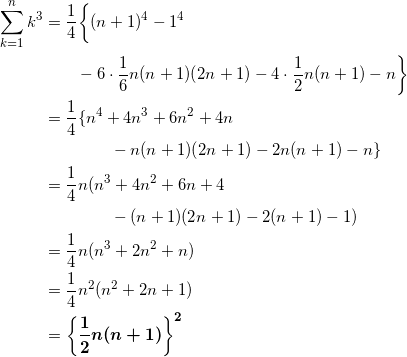
となる。

解説

和の公式の基本は、階差！階差！階差！！

　この問題、ノーヒントでは非常に難しい問題です。シグマ公式は覚えるだけでも高校生を悩ませる1つですが、その成り立ちを知っている人はほとんどいないのではないでしょうか。
　実は和の公式は「階差を作ってうまく消えていくようにする」というところに尽きます。それが(2)や(3)の証明なのですが、そのことを知っていても、教科書の証明を一度でも真似して実際に手を動かしていないと厳しいです。

ちょっと卑怯な方法

　「答えは知ってるけど、証明ができないなあ…」という人は、数学的帰納法を用いた次のような方法も立派な証明法である。
　出題者の意図は「求める過程を示せ」ということかもしれませんが、問題文は“証明を記せ”なので、これでもきちんとした証明になります。ちょっと卑怯かもしれませんが、これを思いつくのも数学的思考力がないとできません。

別解

(1)　

(※) $1 + 2 + \cdots + n = \frac{1}{2}n(n+1)$

が成り立つことを数学的帰納法で示す。

(i)　n = 1 のときは、（左辺） = 1 = （右辺）となり成立。

(ii)　n = k のとき成立することを仮定すると、 n = k + 1 のとき、

$\begin{align*} &(1+ 2+ \cdots + k) + k+1 \\ &= \frac{1}{2}k(k+1) + k+1 \\ &=\frac{1}{2}( k^2 + k + 2k + 2 ) \\ &=\frac{1}{2}(k^2 + 3k +2 ) \\ &=\frac{1}{2}(k+1)(k+2) \end{align*}$

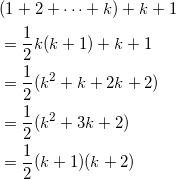
となることから、 n = k + 1 のときも成立することが示された。

(i)、(ii)から、数学的帰納法により(※)が成り立つことが示された。
　
(2)、(3)は省略しますが、同様に解くことができますし、上で示した解答より計算量も少なくスマートですね。

類題

　2014年の大分大の問題も見ておこう。こちらは誘導があるので、手をつけるだけならこちらのほうが簡単です。ただし、(4)は計算が大変で、特に最後の方の因数分解は因数定理を利用してうまく因数分解する必要があります。一度は手を動かして計算してみてください（解答では少し途中を省略しました）。

数列の和について次の一連の問いに答えなさい。
(1)　 $\displaystyle \sum_{k=1}^n k =\frac{1}{2}n(n+1)$ を示しなさい。
(2)　多項式 ( k + 1 )³ – k³ の展開を利用して $\displaystyle \sum_{k=1}^n k^2 = \frac{1}{6}n(n+1)(2n+1)$ を示しなさい。
(3)　 $\displaystyle \sum_{k=1}^n k^3 =\frac{1}{4}n^2(n+1)^2$ を示しなさい。
(4)　 $\displaystyle \sum_{k=1}^n k^4$ を求めなさい。結果は因数分解すること。

［2014 大分大・医］

解答

(1)、(2)、(3)は上の問題と同じなので省略します。

(4)
　　( k + 1 )⁵ – k⁵ = 5k⁴ + 10k³ + 10k² + 5k + 1
を k = 1 から k = n まで書き下して辺々足すと、

$(n+1)^5 - 1^5 = 5\sum_{k=1}^n k^4 + 10 \sum_{k=1}^n k^3 + 10 \sum_{k=1}^n k^2 + 5 \sum_{k=1}^n k + n$

となる。(1)、(2)、(3)の結果を用いて整理すると、

$\begin{align*} 5\sum_{k=1}^n k^4 &= (n+1)^5 - 1 - 10 \left\{ \frac{1}{2}n(n+1) \right\}^2 \\ &\qquad \qquad -10 \cdot \frac{1}{6}n(n+1)(2n+1) - 5 \cdot \frac{1}{2}n(n+1) - n \\ &=\cdots \\ &=\frac{1}{6}n(6n^4 + 15n^3 + 10n^2 - 1) \\ &=\frac{1}{6}n(n+1)(2n+1)(3n^2 + 3n -1) \end{align*}$

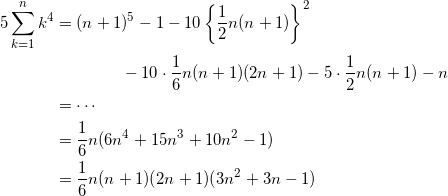
となるので、

$\sum_{k=1}^n k^4 = \bm{\frac{1}{30}n(n+1)(2n+1)(3n^2 +3n-1)}$

Σkⁿは n + 1 次式で、最高次の係数は 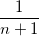$\displaystyle \frac{1}{n+1}$

　今回の問題、例題で求めたシグマ公式（n乗和）をまとめてみると、少し規則が見えてくる。

$\begin{align*} &\sum_{k=1}^n k = \frac{1}{2} n(n+1) = \frac{1}{2}n^2 + n \\ &\sum_{k=1}^n k^2 = \frac{1}{6} n(n+1)(2n+1) = \frac{1}{3}n^3 + \cdots \\ &\sum_{k=1}^n k^3 = \left\{ \frac{1}{2}n(n+1) \right\}^2 = \frac{1}{4}n^4 + \cdots \\ &\sum_{k=1}^n k^4 = \frac{1}{30}n(n+1)(2n+1)(3n^2 +3n+1) = \frac{1}{5}n^5 + \cdots \end{align*}$

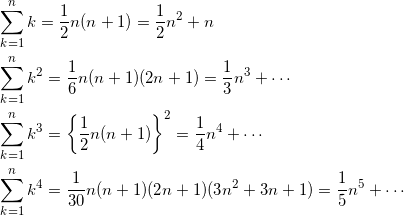
　n乗和の公式は、きれいに統一した形で求められそうにもない。しかし、その公式を展開した式や、その最大次の項に着目すると、

n乗和の公式はすべて多項式で表される
その多項式の次数は、n + 1
さらにその最大次数の係数は $\displaystyle \frac{1}{n+1}$

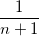
となっていることが分かります。
　このことを証明するのは少し難しそうですが、2006年の東京大学の入試問題にこれを示す出題がある。これは別ページで取り上げよう。

数列の和に関する性質［2006 東京大・理（後）］

数列の和の性質に関する難問です。

連続積の和

　シグマ公式には、高校ではあまり学ばない次の公式がある。

【シグマの和の公式(2)】

$\begin{align*} &\sum_{k=1}^n k = \frac{1}{2}n(n+1) \\ &\sum_{k=1}^n k(k+1) = \frac{1}{3}n(n+1)(n+2) \\ &\sum_{k=1}^n k(k+1)(k+2) = \frac{1}{4}n(n+1)(n+2)(n+3) \end{align*}$

　イズミも「こんなの覚える人いるの？」と思っていたが、最も基礎的な公式である $\displaystyle \sum_{k=1}^n k = \frac{1}{2}n(n+1)$ から派生していっていると考えれば、覚えやすいのではないでしょうか。

$\sum_{k=1}^n k = \frac{1}{2}n(n+1)$

　　　↓　分子が1増えて、掛け算が n , n + 1 , n + 2 となる

$\sum_{k=1}^n k(k+1) = \frac{1}{3}n(n+1)(n+2)$

　　　↓　分子が1増えて、掛け算が n , n + 1 , n + 2 , n + 3 となる

$\sum_{k=1}^n k(k+1)(k+2) = \frac{1}{4}n(n+1)(n+2)(n+3)$

　さて、この式がどのように生まれたのかを紹介していこう。ここで思い出してほしいのが、「シグマ公式の基本は、階差！」ということ。階差をうまく作れれば、和が求められるということなのです。
　そこで、

$k = \frac{1}{2}\{ k(k+1) - (k-1)k \}$

という式を考えてみます。この式において k = 1 から n までの辺々和を取ると、

$\sum_{k=1}^n k = \frac{1}{2}n(n+1)$

が求められます。（これは、本問の(1)の別解ともなります。）

　これを拡張して、

$k(k+1) = \frac{1}{3} \{ k(k+1)(k+2) - (k-1)k(k+1) \}$

という式を考えます。（右辺を展開すると、 k ( k + 1 ) になることはすぐ確認できます。）
　これを同じように k = 1 から n まで辺々和を取ると、先に見た式が求められます。

　文字が増えた式も同じように求められます。簡単なのでやってみてください。

　最後に、この知識をふんだんに利用できる例題を紹介しよう。

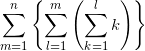　 $\displaystyle \sum_{m=1}^n \left\{ \sum_{l=1}^m \left( \sum_{k=1}^l k \right) \right\}$ は n の多項式になる。この多項式を因数分解せよ。

［1966 一橋大］

解答1

（普通の公式を使って解く）

$\begin{align*} \sum_{m=1}^n \left\{ \sum_{l=1}^m \left( \sum_{m=1}^l k \right) \right\} &=\sum_{m=1}^n \left\{ \sum_{l=1}^m \frac{l(l+1)}{2} \right\} \\ &=\frac{1}{2} \sum_{m=1}^n \left\{ \sum_{l=1}^m (l^2+l) \right\} \\ &=\frac{1}{2} \sum_{m=1}^n \left\{ \frac{1}{6}m(m+1)(2m+1) + \frac{1}{2}m(m+1) \right\} \\ &=\frac{1}{12} \sum_{m=1}^n \{ 2m^3 +3m^2 +m+3(m^2+m) \} \\ &=\frac{1}{6} \sum_{m=1}^n (m^3 + 3m^2 +2m) \\ &=\frac{1}{6} \left\{ \frac{1}{4}n^2(n+1)^2 + 3 \cdot \frac{1}{6}n(n+1)(2n+1) + 2 \cdot \frac{1}{2}n(n+1) \right\} \\ &=\frac{1}{24}n(n+1) \{ n(n+1) + 2(2n+1) + 4\} \\ &=\frac{1}{24}n(n+1) (n^2 + 5n+6)\\ &=\bm{\frac{1}{24} n(n+1)(n+2)(n+3)} \end{align*}$

　これだけのパワープレイ（計算量）ですが、連続積の和の公式を使うと、簡単に解くことができます。

解答2

（連続積の和の公式を使って解く）

イズミの解答への道

解答

解説

和の公式の基本は、階差！階差！階差！！

ちょっと卑怯な方法

別解

類題

解答

Σknは n + 1 次式で、最高次の係数は

連続積の和

解答1

解答2

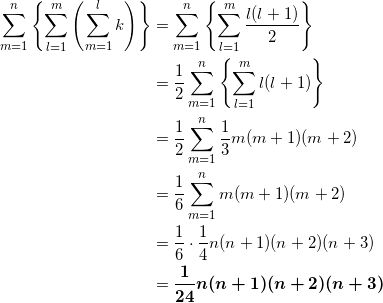
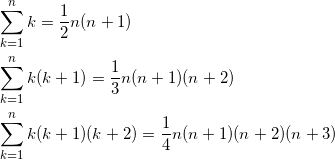
コメント

Σkⁿは n + 1 次式で、最高次の係数は $\displaystyle \frac{1}{n+1}$