問題
(1) cos 5θ = f ( cos θ ) をみたす多項式 f ( x ) を求めよ。
(2) ![]() を示せ。
を示せ。
イズミの解答への道
解答
(1) 加法定理より、
cos 5θ = cos 3θ cos 2θ – sin 3θ sin 2θ
である。ここで、 cos θ = c , sin θ = s とおくと、
cos 2θ = 2c2 – 1
cos 3θ = -3c + 4c3
sin 2θ = 2cs
sin 3θ = 3s – 4s3
= s { 3 – 4 ( 1 – c2 ) }
= s ( 4c2 – 1 )
となるから、
cos 5θ = ( 4c3 – 3c ) ( 2c2 – 1 ) – s ( 4c2 – 1 ) ・ 2cs
= 16c5 – 20c3 + 5c
となることより、求める f ( x ) は、
f ( x ) = 16x5 – 20x3 + 5x
(2) 0 ≦ θ ≦ π の範囲で、
cos 5θ = 0 ……?
を満たすのは、
![]()
である。これらは、すべて異なる値であるから、これらは?の解である。よって、
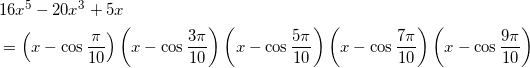
と因数分解でき、このうち、 ![]() であることから、両辺の x を約分して、
であることから、両辺の x を約分して、
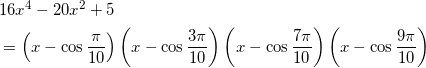
となる。ここで解と係数の関係より、定数項を比較して、
![]()
となることが示された。
解説
チェビシェフの多項式
類題1
まずは、上の問題とほとんど同じパターンで解くことができる問題です。
テスト
テスト
【解答】

コメント