問題
解答
アイウエオ
2次関数の頂点
2次関数の頂点は平方完成して求める
平方完成すると、
y=x2 + 2ax + 3a2 – 6a – 36
= ( x + a )2 + 2a2 – 6a – 36
であるから、頂点は
( –a, 2a2 – 6a – 36 ) …(a)
である。
カキク
問題文より、pはGのy切片であり、与えられた式にx=0を代入して、
p = 3a2 – 6a – 36 …(b)
である。よって、
3a2 – 6a – 36 = -27
3a2 – 6a – 9 = 0
a2 – 2a – 3 = 0
( a+ 1 ) ( a – 3 ) = 0
となり、 a = 3, -1 である。
ケコ
平行移動は、頂点の移動を考える
(a)式を用いて、
- a=3のときの頂点は、
( -3 , 2・32 – 6・3 – 36 ) = ( -3 , -36 )
- a=-1のときの頂点は
( – ( -1 ) , 2・(-1)2 – 6・( -1 ) – 36 ) = ( 1 , -28 )
より、 ( -3 , -36 ) を ( 1 , -28 ) に移動するために、x方向に4、y方向に8移動すれば良い。
サシスセソ
x軸との共有点は、y = 0 との連立方程式で考える
x軸と共有点を持つということは、連立方程式
y=x2 + 2ax + 3a2 – 6a – 36
y=0
すなわち
x2 + 2ax + 3a2 – 6a – 36 = 0
が解を持つということである。それは判別式を考えて、
D/4 = a2 – ( 3a2 – 6a – 36 ) ≧ 0
-2a2 + 6a + 36 ≧ 0
a2 – 3a – 18 ≦ 0
( a + 3 )( a – 6 ) ≦ 0
より、
-3 ≦ a ≦ 6 …(c)
が正解。(スセはともに。)
タチツテトナニ
問題文と(b)式より、
p = 3a2 – 6a – 36 ( -3 ≦ a ≦ 6 )
の最大値と最小値を求める。
p = 3 ( a – 1 )2 – 39
より、
a=1のとき最小値-39
a=5のとき最大値36
をとる。
ヌネノハヒフヘ
解の配置問題?解の配置は3条件
-1より大きいところで交わるためには、
- 解を持つ条件:判別式が正
- 軸の条件:軸のx座標が-1より大きい
- ポイントの条件:x=-1のときのyの値が正
を調べれば良い。
1つ目の判別式はすでに解いており、(c)より、
-3 ≦ a ≦ 6 …改めて(c)
2つ目の条件は、軸の x 座標が -1 より大きいことより、 -a ≧ -1 すなわち
a ≦ 1 …(d)
3つ目の条件は、 x = -1 のときに y > 0 を満たしていればよく、
(e) 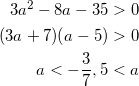

コメント