以下のように、歩行者と自転車が自宅を出発して移動と停止を繰り返している。歩行者と自転車の動きについて、数学的に考えてみよう。
自宅を原点とする数直線を考え、歩行者と自転車と自転車をその数直線上を動く点とみなす。数直線上の点の座標が y であるとき、その点の位置 y にあるということにする。また、歩行者が自宅を出発してから x 分経過した時点を時刻 x と表す。歩行者は時刻 0 に自宅を出発し、正の向きに毎分 1 の速さで歩き始める。自転車は時刻 2 に自宅を出発し、毎分 2 の速さで歩行者を追いかける。自転車が歩行者に追いつくと、歩行者と自転車はともに 1 分だけ停止する。その後、歩行者は再び正の向きに毎分 1 の速さで歩き出し、自転車を毎分 2 の速さで自宅に戻る。自転車は自宅に到着すると、 1 分だけ停止した後、再び毎分 2 の速さで歩行者を追いかける。これを繰り返し、自転車は自宅と歩行者の間を往復する。
x = an を自転車が n 回目に自宅を出発する時刻とし、 y = bn をそのときの歩行者の位置とする。
(1) 花子さんと太郎さんは、数列 { an } , { bn } の一般項を求めるために、歩行者と自転車について、時刻 x において位置 y にいることを O を原点とする座標平面上の点 ( x , y ) で表すことにした。
a1 = 2 , b1 = 2 により、自転車が最初に自宅を出発するときの時刻と自転車の位置を表す点の座標は ( 2 , 0 ) であり、そのときの時刻と歩行者の位置を表す点の座標は ( 2 , 2 ) である。また、自転車が最初に歩行者に追いつくときの時刻と位置を表す点の座標は ( ア , ア ) である。よって
a2 = イ , b2 = ウ
である。
花子:数列 { an } , { bn } の一般項について考える前に、( ア , ア ) の求め方について整理してみようか。
太郎:花子さんはどうやって求めたの?
花子:自転車が歩行者を追いかけるときに、感覚が 1 分間に 1 ずつ縮まっていくことを利用したよ。
太郎:歩行者と自転車の動きをそれぞれ直線の方程式で表して、交点を計算して求めることもできるね。
自転車が n 回目に自宅を出発するときの時刻と自転車の位置を表す点の座標は ( an , 0 ) であり、そのときの時刻と歩行者の位置を表す点の座標は ( an , bn ) である。よって、 n 回目に自宅を出発した自転車が次に歩行者に追いつくときの時刻と位置を表す点の座標は an , bn を用いて、 ( エ , オ ) と表わせる。
エ , オ の解答群(同じものを繰り返し選んでもよい。)
⓪ an ① bn ② 2an
③ an + bn ④ 2bn ⑤ 3an
⑥ 2an + bn ⑦ an + 2bn ⑧ 3bn
以上から、数列 { an } , { bn } について、自然数 n に対して、関係式
an+1 = an + カ bn + キ ……①
bn+1 = 3bn + ク ……②
が成り立つことが分かる。まず、 b1 = 2 と②から
bn = ケ ( n = 1 , 2 , 3 , … )
を得る。この結果と、 a1 = 2 および①から
an = コ ( n = 1 , 2 , 3 , … )
がわかる。
ケ , コ の解答群(同じものを繰り返し選んでもよい。)
⓪ 3n-1 + 1 ① 12・3n + 12
② 3n-1 + n ③ 12・3n + n – 12
④ 3n-1 + n2 ⑤ 12・3n + n2 – 12
⑥ 2・3n-1 ⑦ 52・3n-1 – 12
⑧ 2・3n-1 + n – 1 ⑨ 52・3n-1 + n – 32
ⓐ 2・3n-1 + n2 – 1 ⓑ 52・3n-1 + n2 – 32
(2) 歩行者が y = 300 の位置に到達するときまでに、自転車が歩行者に追いつく回数は サ 回である。また、 サ 回目に自転車が歩行者に追いつく時刻は x = シスセ である。
解答
ア
歩行者と自転車の速度の差は1分間に1である。自転車が最初に自宅を出発するとき、歩行者と自転車との距離の差は 2 であるから、自転車が最初に歩行者に追いつくまでには 時間が 2 かかる。よって、追いつく時刻は 4 であり、その時の位置は 4 である。
よって、自転車が最初に歩行者に追いつくときの時刻と位置を表す点の座標は ( 4 , 4 ) である。
イウ
時刻 4 以降の自転車の動きを考える。このあと1分間歩行者とともに休んだあと、自宅へと戻る。自宅へ戻るのにかかる時間は、追いつくのにかかった時間と同じで 2 分である。このあと1分間休んだあと出発するので、
a2 = 4 + 1 + 2 + 1 = 8
である。
歩行者は、8分間のうち1分だけ休んでいるので、 b2 = 7 である。
エオ
n回目に自宅を出発する時点で、歩行者と自転車との距離の差は bn である。この差を縮めるのに bn 分かかるので、n回目に自転車が歩行者に追いつく座標の x 座標は
③ an + bn
である。歩行者は位置 bn からさらに bn だけ進むので、求める座標の y 座標は
④ 2bn
である。
※これはあとでも使うので、名前をつけて整理しておきましょう。 n 回目に自転車が歩行者に追いつく座標を ( pn , qn ) とすると、
pn = an + bn
qn = 2bn
カキク
n回目に自転車が歩行者に追いついた時間から、休憩1分、戻るのにbn分、さらに休憩1分して、 n + 1 回目の出発となるので、
an+1 = pn + 1 + bn + 1
=( an + bn ) + 1 + bn + 1
= an + 2bn + 2
である。歩行者は、自転車が戻るのにかかる時間bn と休憩1分の間あるき続けるので、
bn+1 = qn + bn + 1
= 2bn + bn + 1
= 3bn + 1
となる。
ケ
漸化式 bn+1 = 3bn + 1 を解く。
(特性方程式 x = 3x + 1 を解いて x = -1/2 なので、)与えられた漸化式は、
bn+1 + 12 = 3 ( bn + 12 )
と変形できるので、数列 { bn + 12 } は、初項 b1 + 12 = 52 、公比 3 の等比数列。よって、
bn + 12 = 52・3n-1
より、
bn = 52・3n-1 – 12
である。選択肢は⑦。
コ
この結果を式①に代入すると、漸化式 an+1 = an + 5・3n-1 + 1 を得る。この漸化式は階差数列なので、 n ≧ 2 のとき、
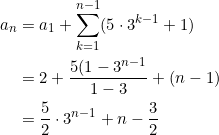
となる。(なお、 n = 1 のとき a1 = 2 となり n = 1 のときも満たす。)選択肢は⑨。
サシスセ
自転車が歩行者に n 回目に追いつくときの位置( y 座標)は qn = 2bn であるから、これが300以下になればよい。
b2 = 7 , b3 = 22 , b4 = 67 , b5 = 202 , b6 = 607
より、 5回目に追いつく位置は 2b5 = 404となってしまうので、 y = 300 までに追いつく回数は 4 回。
4回目に追いつく時刻は、
p4 = a4 + b4 = 137
である。

コメント