2通りの解法で解く［2021 浜松医科大］

(1) AB = 4 , AC = 3 である三角形ABCの辺BCを 2 : 1 に内分する点をDとする。また、AD = 1 とする。
(a) BCの長さを求めよ。
(b) (a)とは別の解法でBCの長さを求めよ。

［2021浜松医科大］

イズミの解答への道

　問題自体は簡単な問題ですが、非常に良い問題です。
　数学ではよく、基本を終えた生徒に対して「いろんな解き方を考えてみましょう」「別解を考えてみましょう」という指導がなされます。まさにそれを突いた出題で、2つ目の解法を思いつけるかどうかということは、少なくとも中級者以上まで勉強していますよね、ということを確認できるということです。

　さて、今回の問題は図形の問題ですから、図形のまま解く（三角比もしくは平面幾何として解く）以外に、「ベクトルで解けないか？」「座標平面設定して解けないか？」あたりは定番として思いつくようにしておきたいところです。（解説に書きますが、図形の問題を図形以外の方法で解く、というのは京都大学入試での頻出テーマです。）

解答

　(a)、(b)ともに、以下の解答のいずれかを挙げればよい。

三角比の知識で解く

　BD = 2t , DC = t ( t > 0) とおく。
　△ABDと△ABCについて余弦定理を用いてcos∠Bを求めると、
　　cos∠B = 4t² + 16 – 12・2t・4 = 9t² + 16 – 92・3t・4
を整理して、
　　3 ( 4t² + 15 ) = 2 ( 9t² + 7 )
を解いて、
　　6t² = 31
　　t = √1866
である。よって、
　　BC = 3t = √1862

ベクトルで解く

内分点の公式を使えるかたちでベクトルを設定する

　Dは線分ABを2:1に内分する点なので、内分点の公式より、
　　 $\displaystyle \overrightarrow{\text{AD}} = \frac{1}{3}\overrightarrow{\text{AB}} +\frac{2}{3}\overrightarrow{\text{AC}}$
と置けるのでこれを辺々二乗して
　　 $\displaystyle |\overrightarrow{\text{AD}}|^2 = \frac{1}{9}|\overrightarrow{\text{AB}}|^2 + \frac{4}{9} \overrightarrow{\text{AB}} \cdot \overrightarrow{\text{AC}} +\frac{4}{9}|\overrightarrow{\text{AC}}|^2$
となり、これを整理すると、
　　 $\displaystyle \overrightarrow{\text{AB}} \cdot \overrightarrow{\text{AC}} = -\frac{43}{4}$
となる。

　求める長さは $\displaystyle |\overrightarrow{\text{BC}}|$ なので、

$\begin{align*} |\overrightarrow{\text{BC}}|^2 &= |\overrightarrow{\text{AC}} - \overrightarrow{\text{AB}}|^2 \\ &=|\overrightarrow{\text{AC}}|^2 - 2 \overrightarrow{\text{AB}} \cdot \overrightarrow{\text{AC}} + |\overrightarrow{\text{AB}}|^2 \\ &=9 + \frac{43}{2} + 16 = \frac{93}{2} \end{align*}$

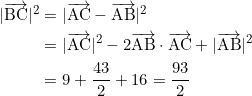
となるので、　BC = √1862 となる。

座標平面を設定して解く

内分点、外分点がある場合は、その点を原点におくのが定石

　△ABCを座標平面上に設定する。点Dを原点におくと、 t ( > 0 ) を用いて、
　　D ( 0 , 0 ) , B ( -2t , 0 ) , C ( t , 0 )
とおける。
　DA = 1 であるから、Aは原点を中心とした半径 1 の円周上にあるので、
　　A ( cosθ , sinθ )
とおくことができる。

　いま、AB = 4 , AC = 3 であることから、三平方の定理より、
　　( cosθ + 2t )² + sin²θ = 16
　　( cosθ – t )² + sin²θ = 9
となる。これを整理すると
　　4t cosθ + 4t² = 15……①
　　-2t cosθ + t² = 8……②
となり、 ①＋②×2 より、
　　6t² = 31
　　t = √1866
を得る。よって、
　　BC = 3t = √1862