自然数 n に対して、関数 fn ( x ) = xn e1-x と、その定積分 ![]() を考える。ただし、 e は自然対数の底である。次の問いに答えよ。
を考える。ただし、 e は自然対数の底である。次の問いに答えよ。
(1) 区間 0 ≦ x ≦ 1 上で 0 ≦ fn ( x ) ≦ 1 であることを示し、さらに 0 < an < 1 が成り立つことを示せ。
(2) a1 を求めよ。 n > 1 に対して an と an-1 の間の漸化式を求めよ。
(3) 自然数 n に対して、等式
![]()
が成り立つことを証明せよ。
(4) いかなる自然数 n に対しても、 n ! e は整数とならないことを示せ。
[1997 大阪大・理(後)]
イズミの解答への道
誘導どおりに解いていけば、(2)まで詰まることはないでしょう。(2)の漸化式を解いて一般項を求められればよいのですが、これは一筋縄には行きません。しかし、求める式が与えられているので最悪でも“数学的帰納法”でなんとかしましょう。(3)までできれば(4)はもうすぐそこ。
解答
(1) f’n ( x ) = n xn-1 e1-x + xn (-e1-x)
=e1-x xn-1 ( n – x ) ≧ 0
より fn ( x ) は単調増加であり、 fn ( 0 ) = 0 , fn ( 1 ) = 1 であるから、
0 ≦ x ≦ 1 で 0 ≦ fn ( x ) ≦ 1
である。
また、![]() は、区間 0 ≦ x ≦ 1 における y = fn (x) と x 軸に挟まれた面積であり、
は、区間 0 ≦ x ≦ 1 における y = fn (x) と x 軸に挟まれた面積であり、
![]()
が成り立つので、これより、![]() も示される。
も示される。
(2) 部分積分より、
![Rendered by QuickLaTeX.com \begin{align*} a_1 &= \int_0^1 xe^{1-x} dx \\ &=\left[ x (-e^{1-x}) \right]_0^1 - \int_0^1 ( -e^{1-x} ) dx \\ &=\left[ - x e^{1-x} \right]_0^1 + \int_0^1 e^{1-x} dx \\ &= -1 - \left[ e^{1-x} \right]_0^1 \\ &= -1 -(1-e) = \bm{e-2} \end{align*}](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-88b435510cd638684231c28f08d507d0_l3.png)
であり、
![Rendered by QuickLaTeX.com \begin{align*} a_n &= \int_0^1 x^n e^{1-x} dx \\ &=\left[ x^n ( -e^{1-x}) \right]_0^1 - \int_0^1 \{ nx^{n-1} \cdot (-e^{1-x}) \} dx \\ &=\bm{-1 + na_{n-1}} \end{align*}](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-9a5bd04d1d58fb7ef5a993e4b6af484c_l3.png)
となる。
(3) 数学的帰納法で示す。
(i) n = 1 のとき、
![]()
より、 a1 = e – 2 であり、これは(2)の結果と一致する。
(ii) n = k のときに成り立つとする、すなわち、
![]()
が成り立つとしたとき、
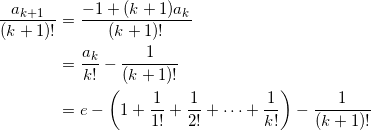
より、題意の等式は n = k + 1 のときも成り立つ。
以上より、すべての自然数 n について第位の等式が成り立つことが示された。
(4) (3)より、
![]()
である。ここで、![]() より、 an は整数ではなく、
より、 an は整数ではなく、![]() は整数であるから、
は整数であるから、 ![]() は整数ではないといえる。
は整数ではないといえる。
解説
eが無理数であることの証明
e が有理数であると仮定すると、![]() ( p , q は自然数) と表される。いま、
( p , q は自然数) と表される。いま、
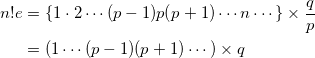
は整数となるが、(4)の結果に反する。よって背理法により、 e は無理数であることが示された。
eを無限和で表す
(1)の結果と(3)で導かれた等式より、![]() であるから、これを n → ∞ のはさみうちから、
であるから、これを n → ∞ のはさみうちから、
![]()
すなわち、
![]()
ということができる。これを ex の x = 0 におけるテイラー展開(すなわちマクローリン展開)という。

コメント