複素数 an ( n = 1 , 2 , … ) を次のように定める。
![]()
ただし、 i は虚数単位である。このとき以下の問いに答えよ。
(1) 複素数平面上の3点 0 , a1 , a2 を通る円の方程式を求めよ。
(2) すべての an は(1)で求めた円上にあることを示せ。
[2005 北海道大・理]
イズミの解答への道
(1)では、漸化式で与えられた3点が円上にあることを示し、(2)ではその漸化式で与えられるすべての点が(1)の円上にあることを示す、という流れ。(1)は具体的に計算をし、(2)は数学的帰納法で証明するのがポイント。
適当な数列ではそのようなことにはならないが、問題で与えられる数列は「必ず円上にあるように」仕組まれている数列なので、がむしゃらに計算をしてもうまく収まるようにできている。実際に(2)の後半でそれを感じてもらいたい。
解答
(1) 与えられた式より、
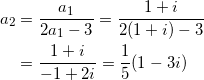
となる。
以下は平面座標で考える。原点、 ( 0 , 0 ) 、![]() を通る、中心 ( p , q ) 、半径 r の円は、
を通る、中心 ( p , q ) 、半径 r の円は、
![Rendered by QuickLaTeX.com \[ \begin{cases} p^2 + q^2 = r^2 & \text{$\cdots$(a)} \\ ( 1-p)^2 + (1-q)^2 = r^2 & $\cdots$ \text{(b)} \\ \displaystyle \left( \frac{1}{5} - p \right)^2 + \left( -\frac{3}{5} - q \right)^2 = r^2 &\text{$\cdots$(c)}\end{cases} \]](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-e223e0ed295c0e895ce15628e8d66f6f_l3.png)
を満たす。(b)式、(c)式はそれぞれ
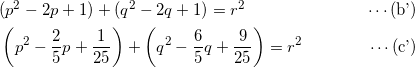
である。(b’)-(a)より、
-2p – 2q +2 = 0
すなわち、
p + q = 1 …(d)
であり、同様に(c’)-(a)より、
![]()
すなわち、
p – 3q = 1 …(e)
であり、(d)と(e)の連立方程式を解いて、
p = 1, q = 0
を得る。このとき r = 1 であるから、求める円は ( 1 , 0 ) を中心とした半径 1 の円。複素数平面では、求める円の方程式は、
| z – 1 | = 1
である。
(2) すべての n について、
| an – 1 | = 1 …(※)
が成り立つことを数学的帰納法によって示す。
(i) n = 1 のときは(1)で示したとおり成立する。
(ii) n = k のとき(※)が成立すると仮定すると、
| ak – 1 | = 1
⇔| ak – 1 |2 = 1
⇔![]() …(f)
…(f)
が成り立つ。
いま、
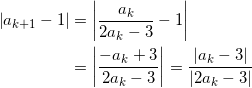
が成り立つ。ここで、
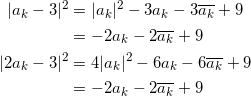
となることから、 | ak – 3| = |2ak | であるから、
![]()
となり、 n = k + 1 のときも(※)が成り立つ。
以上、(i)、(ii)より数学的帰納法によってすべての n によって(※)が成り立つことが示された。
よって、すべての anは中心 1 、半径 1 の円周上にあることが示された。
解説
(2)の別解
数学的帰納法で示すところは同じ。(ii)で n = k のときに成立すると仮定すると、
| ak – 1 | = 1
が成り立つ。
いま、
![]()
の両辺の逆数を取って
![]()
となることから、
![]()
となるので、
![]()
が成り立つ。
| ak – 1 | = 1 であったから、
![]()
が成り立ち、
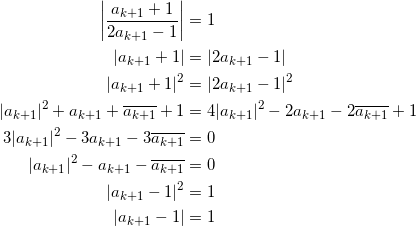
となる。よって、 ak+1 も 中心 1 、半径 1 の円周上にあることが示される。以下は同じ。
類題
この問題を解けるようになると、次の東大の問題も同じように解くことができます。
複素数平面上の点 a1 , a2 , … , an , … を
![Rendered by QuickLaTeX.com \[ \begin{cases} a_1 =1 , a_2 = i \\ a_{n+2} = a_{n+1} + a_n \quad ( n = 1 ,2 ,\cdots) \end{cases} \]](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-32119a6638a5bb8bd70108829db5fa95_l3.png)
により定め
![]()
とおく。ただし、 i は虚数単位である。
(1) 3点 b1 , b2 , b3 を通る円Cの中心と半径を求めよ。
(2) すべての点 bn ( n = 1, 2, … ) は円Cの周上にあることを示せ。
[2001 東京大・理]
【解答】
(1) a1 = 1 , a2 = i , a3 = 1 + i , a4 = 1 + 2i
であるから、
![]()
である。
以下は平面座標上で考える。中心 ( p , q ) 、半径 r の円が、3点 ( 0 , 1 ) , ( 1 , -1 ) , ![]() を通るとき、
を通るとき、
![Rendered by QuickLaTeX.com \[ \begin{cases} p^2 + (1-q)^2 = r^2 \\ (1-p)^2 + (1+q)^2 = r^2 \\ \displaystyle \left( \frac{3}{2} -p \right)^2 + \left(\frac{1}{2}-q \right)^2 = r^2 \end{cases} \]](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-c2d4de598937aa8fa492e1f684fa457c_l3.png)
であり、これを計算して解くと、 ![]() であり、このとき
であり、このとき![]() となるので、
となるので、
求める円Cの中心は ![]() 、半径は
、半径は ![]()
である。
(2) すべての点 bn ( n = 1, 2, … ) は円Cの周上にあることを数学的帰納法によって示す。
(i) n = 1 のとき
(1)より、 b1 は(1)より円Cの周上にある。
(ii) n = k のとき題意を満たすと糧する。つまり、 bk は円Cの周上にあるとすると、
![]()
が成り立つ。これより、
(a) ![]()
が成り立つ。
次に、 n = k + 1 のときを考える。漸化式より、
![]()
が成り立つ。いま、![]() の値を考えると、
の値を考えると、
![]()
であり、(a)を用いると、
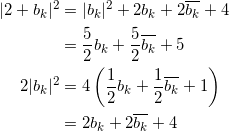
となり、
![]()
すなわち、
![]()
である。よって、
![]()
となるので、 bk+1 も円Cの周上にある。
(i)、(ii)より、すべての点 bn ( n = 1, 2, … ) は円Cの周上にあることが数学的帰納法により示された。
※この問題の(2)も別解で示したように、 bk = の形に変形して解くことも可能である。これも各自試してもらいたい。

コメント