次の問いに答えよ。
(1) r , s を r < s である有理数とするとき、 r < c < s を満たす無理数 c が存在することを示せ。
(2) α , β を α < β である実数とするとき、 α < q < β を満たす有理数 q が存在することを示せ。
(3) x を有理数の定数とする。このとき、不等式 | x – nm | < 1m2 をみたすような自然数 m と整数 n を用いて nm の形に表すことができる有理数は有限個であることを示せ。
(4) 条件式 a1 = a2 = 1 , an+2 = an+1 + an ( n = 1 , 2 , 3 , …… )により数列 { an } を定め、 ![]() とする。不等式
とする。不等式
![]()
を示せ。
[2016 大阪大・専門数学]
イズミの解答への道
(1)と(2)は、簡単に証明できそうで、なかなか難しい。特に(2)は一捻り必要。実は大学より先で数学を学ぶ上では大事なテーマが隠されており、(2)の証明には解説で示す別解がよく知られている。これを知っておくとよいだろう。
(3)はうってかわって、題意を満たす数が有限個だけ存在することの証明。「有限個の証明」というのは高校数学ではなかなか扱わないので、これも証明が難しかったかもしれない。
(4)は(3)を使って解くのかと思いきや、 x が有理数でないところでさっそく断念。(4)も独立して解く必要があります。ただし、(4)が最も高校数学らしい問題だったかもしれない。なお、小問が4つ並んでいるが、この4問は特別関係しあってはいない。(4)だけ解くことも可能である。
解答
(1) r , s を![]() に内分する点 c を考える。
に内分する点 c を考える。
![]()
とすると、c は内分点であるから明らかに r < c < s を満たしており、 r , s は有理数かつ r ≠ s であることより、 c は無理数。以上より、題意は示された。
(2) 解答調整中
(3) ![]() ( p は自然数、 q は p とは互いに素な整数)とおくと、与えられた式は、
( p は自然数、 q は p とは互いに素な整数)とおくと、与えられた式は、
![]()
となる。
(i) ![]() のとき
のとき
0 ≦ | qm – pn | < 1 となるから、 | qm - pn | = 0 でしかない。すなわち、
![]()
であるから、![]() を表す有理数は
を表す有理数は ![]() だけである(有限個)。
だけである(有限個)。
(ii) ![]() のとき
のとき
条件にしたとおり、 m は有限個である。これらの m のなかから一つの m を固定したとき、
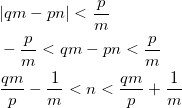
となり、この区間はたかだか ![]() であるから、この区間に含まれる n の個数は有限個となる。
であるから、この区間に含まれる n の個数は有限個となる。
m , n ともに有限個であることから、 ![]() の表す有理数も有限個である。
の表す有理数も有限個である。
以上より、与えられた条件を満たす m , n に対して ![]() の表す有理数は有限個であることが示された。
の表す有理数は有限個であることが示された。
(4) ![]() とおくと、
とおくと、
x + y = 1 , xy = -1
より、与えられた漸化式は
an+2 – ( x + y ) an+1 + xy an = 0
より、
an+2 – x an+1 = y ( an+1 – x an)
an+2 – y an+1 = x ( an+1 – y an)
すなわち、
an+1 – x an = ( a2 – x a1 ) yn-1 = yn …①
an+1 – y an = ( a2 – y a1 ) xn-1 = xn
となるので、この結果より、
![]() …②
…②
となる。
いま、①より、
an+1 – xan = yn
だから、
![]()
すなわち
![]() …③
…③
となる。
さて、ここで、![]() を示そう。②より、
を示そう。②より、
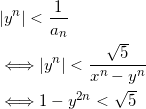
であり、最後の式は ![]() だから成り立つ。よって、
だから成り立つ。よって、![]() も成立する。
も成立する。
これを③に代入して、
![]()
が成立。問題の式は示された。
解説
(2)の別解
高校ではこのような証明を見ることはないが、大学数学ではよくみる手法なので、覚えておいても損はありません。
![]() を満たすような十分大きい自然数 N をとる。このとき、
を満たすような十分大きい自然数 N をとる。このとき、
![]()
すなわち
![]()
となることより、 NβとNαの差は1より大きいので、この間に少なくとも一つの整数が存在する。これを n とおくと、
![]()
![]()
となり、![]() は有理数だから題意が示された。
は有理数だから題意が示された。
有理数の稠密性
有理数のみの世界を考えてみましょう。
2つの有理数の間には、明らかに有理数が存在します。たとえば有理数 a と有理数 b のちょうど真ん中の数は、![]() となり、これは有理数ですね。
となり、これは有理数ですね。
このことを繰り返し使えば、どのような有理数と有理数の間にも有理数があるのだから、数直線上は有理数で埋め尽くされる、ような気がします。(いいかえれば、どのような有理数のすぐ近くにも、別の有理数が存在するということです。なぜなら、ある有理数に対して、もうこれ以上近いところには有理数はないだろう、と思うほど近いところにある有理数を取ってきても、その有理数との間に別の有理数が存在するからです。)
感覚的ですが、この性質のことを稠密性(ちゅうみつせい)といい、有理数は稠密である、有理数は稠密性をもつ、などといいます。
無理数の稠密性
いまの説明を読んで、みなさんはどう思ったでしょうか。「有理数のすぐそばには別の有理数がある、ということは有理数は数直線上に”ぎっしり”存在するんだなあ。」と思った方もいるかと思います。その感想はごくごく自然なものです。
しかし、ここで無理数のことを考えてみましょう。
数直線上には無理数が存在することは明らかですね。そして、(1)で見たように、有理数と有理数の間には無理数もまた存在します。
ですから、一見、数直線は有理数で埋め尽くされるように見えますが、有理数と有理数の間には無理数が、いいかえれば、有理数のすぐ近くには、無理数も存在するということです。つまり、有理数で埋め尽くされているのかといえば、そんなことはなく、無理数で作られる抜けもある、ということです。
なお、任意の二つの無理数の間にも無理数が存在することも容易に証明できますので、無理数も稠密性を持つといえます。また無理数と無理数の間に有理数があることは本問の(2)で証明されました。
有理数、無理数はどちらが多い?(集合の濃度とカントールの対角線論法)
さて、以上のことをまとめてみましょう。
- 有理数だけでみたとき、数直線は有理数で覆い尽くされているようで、実は、無理数の穴がある。
- 無理数だけでみたとき、数直線は無理数で覆い尽くされているようで、実は、有理数の穴がある。
このように見てみると、有理数と無理数の関係は表裏一体のように見えますね。ところで有理数と無理数はどちらがたくさんあるのでしょうか。表裏一体だから、同じぐらい多い、といえるのでしょうか。
どちらも無限にあるので、簡単に数えることはできません。無限集合の大きさ(要素の個数)を考えるときのポイントは、次の2点です。
- 無限集合の大きさは、濃度という概念で考える。
- 集合同士の濃度を1対1対応があるかどうかで
ある無限集合Aの濃度|A|と表す。2つの集合の要素について、1対1対応が付くとき(全単射)、集合の濃度は等しいといい、
|A|=|B|
とあらわします。
一方で、集合 A から B への単射が存在するとき,|A| ≦ |B| とする。

コメント
(2)
『α , β を -α 平行移動した、0 , β – α ( = γ と定義する)として、0 , β – α の間に、 0 < q’ < β – α を満たす有理数 q’ が存在することを示しても差し支えない。』
この方針は駄目です。
0 < q’ < β – α を満たす有理数q'があったとして、このq'を用いるとα < q’+α < βとなりますが、αが無理数だとq’+αもやはり無理数になってしまうので、これでは α < q < βなる有理数qが存在することを示したことになりません。
ほぼ繰り返しですが、αが無理数の場合、α < q < βなる有理数qに対し、q-αは無理数です。
> 通りすがり様
ご指摘ありがとうございました。ご指摘いただいた通りの間違いをしておりました。(表記を楽しようとして、致命的なミスをしていました。)
なんとか代数的に説明したいというのが念頭にあり、今回は素直に、2つの無限小数から間にある有限小数を作り出すことで示す方法に書き直しました。
この方法で証明になりますでしょうか? 考え方に間違いがあれば改めてご指摘いただければありがたいです。
※なお、(3)の記述も今読み返すと下手くそですね。折を見て直させていただきます。
私の先程の反例は「αが無理数の時に先程の論法だと示した事にならない」という事でした。で、問題は「α, βは『実数』」とあって、有理数とも無理数とも言ってません。従って冒頭の「無理数は循環しない無限小数で表されるから、」のところからまず修正の必要があります。
つまり「α は、10nの位が 0 ≦ an ≦9 を満たす整数であるような整数を用いて、
α = …a2a1a0.a-1a-2a-3…
と表すことができる」というのは、(この方針で証明しようとするのなら、)先ずその点を修正する必要があります。が、もう一点問題があって、それはα(やβ)が負の数の時、この表記だと難しいのです(例えば、普通「-2.3の整数部分は-3、小数部分は0.7」として扱いますよね)。
(後、大学数学だと、無理数が十進表記出来る、という事自体が実数体のArchimedes性を使って証明しないといけないので、この問題でそもそも無理数の十進表記を許容しているのかどうかが良く分かりません…)
> 通りすがり様
改めてのご指摘ありがとうございました。
自分で問題文まで打っていて恥ずかしい話ですが、何故か知りませんが勝手に「無理数と無理数の間に有理数がある」ことを示す問題だと勘違いしておりました。
有理数と無理数の場合も似たような方法で説明できるのかもしれませんが、
ご指摘いただいた負の数の場合も場合分けで回避しなければならないなど、説明が非常に長くなってしまい、
こうなるとさすがに別解に示す(まあ、いわゆる普通の方法)のほうが素直な解法だと思えますので、その方法に修正しておきます。
※もともとは、(大学入試ということもあり)この証明を高校生ぐらいの数学のやり方で説明できないかと書いておりました。もしよい証明がありましたら教えていただければと思います。
以上、ご指摘ありがとうございました。