問題
実数 x , y が x2 + y2 = 1 を満たすとき、
![]()
の最小値は であり、最大値は である。
イズミの解答への道
数式だけで行こうとすると、非常に難しい問題。しかし、与えられた条件は円。では図形的に見れば k は何を表しているのでしょうか? 展開してみると、
y – 4 = k ( x – 7 )
となります。ここでピンとくるように練習しておきましょう。
解答
![]() より、
より、
y – 4 = k ( x – 7 ) ……(a)
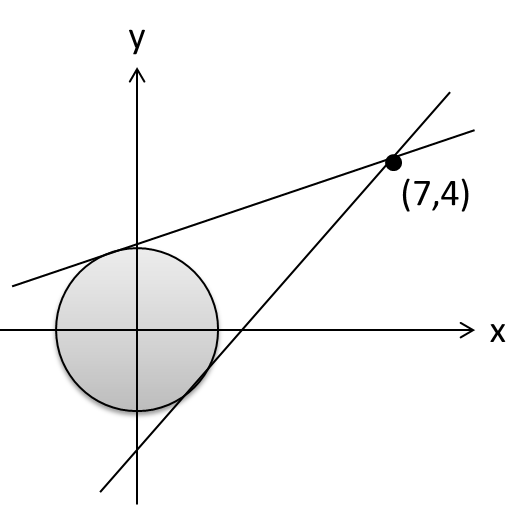
であり、これは座標平面上で ( 7 , 4 ) を通る傾き k の直線である。
x , y は原点中心の半径 1 の円(これを C とする)上にあるから、円Cに接し、( 7 , 4 ) を通る2本の直線の傾きを調べればよい。
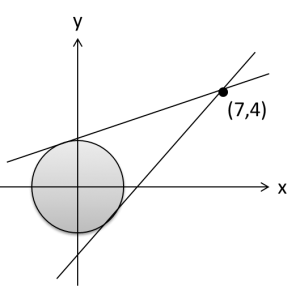
直線 (a)
kx – y – 7k + 4 = 0
と原点の距離が 1 となるような k の値を求めればよく、それは点と直線の公式より、
![]()
を解いて、
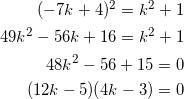
より、![]() 。
。
以上より、k の最小値は ![]() 、最大値は
、最大値は ![]() である。
である。
解説
傾きとしてみる
ここで使った手法は、次のようにまとめられます。
は、 y = f ( x ) 上の点と、点 ( a , b ) を結ぶ直線の傾きを表す。
今回の問題は、 k = の形で与えられているために上の解き方に気付きやすいはずです。それでは次の例題ではどうでしょうか?
関数 ![]() を最大、最小にする x の値を求めよ。
を最大、最小にする x の値を求めよ。
[2002 日本女子大・理]
普通に解くと、関数を微分して最大・最小を求める問題になりますが、ここで今回の手法を用いると、次のように解答することができます。
【解答】
座標の x との混同を防ぐため、問題の x を θ と置き換えて考える。
![]()
は、座標平面上の点 ![]() と単位円上の点 ( cos θ , sin θ )結ぶ直線の傾きである。
と単位円上の点 ( cos θ , sin θ )結ぶ直線の傾きである。
単位円 x2 + y2 = 1 上の点 ( cosθ, sinθ ) における接線は、
x cosθ + y sinθ = 1
であり、これが、 ![]() を通るので、代入して整理すると、
を通るので、代入して整理すると、
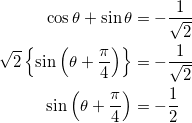
となり、これを解くと、
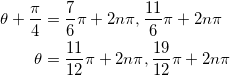
となる。図を考えると、前者が傾きの最大値となり、後者が最小値となることがわかる。最後にθをxに直して、
最大値を与える x は、![]()
最小値を与える x は、![]()
となる。
コメント