![]() を二項係数とするとき、次の和を求めよ。
を二項係数とするとき、次の和を求めよ。
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
[1999 東京理科大・理・応用数]
イズミの解答への道
組み合わせの関係する計算問題は頻出であるが、本問はその中でも最難といえる問題だと考えられる。組み合わせの計算は、二項定理を用いた等式
![]()
を用いて解くのが基本であり、(1)はこれによって解くことができる頻出問題。それ以降については、さてどうするか。
解答
二項定理より、
![]() …①
…①
が成り立つ。
(1) ①に x = 1 を代入すると、
![]()
となる。
(2) ①の両辺に x を掛けて、
![]()
として、これを x で微分すると、
![]()
となり、ここに x = 1 を代入して、
![]()
(3) わかりやすいように①を書き下すと、
![]()
となる。これの両辺を x = 0 から x = 1 の範囲で積分すると、
![Rendered by QuickLaTeX.com \begin{align*} &\left[ {}_n \text{C}_0 x + \frac{1}{2} {}_n \text{C}_1 x^2 + \frac{1}{3} {}_n \text{C}_2 x^3 + \cdots + \frac{1}{n+1} {}_n \text{C}_n x^{n+1} \right]_0^1 = \left[ \frac{1}{n+1} (1+x)^{n+1} \right]_0^1 \\ &{}_n \text{C}_0 + \frac{1}{2}{}_n \text{C}_1 + \frac{1}{3}{}_n \text{C}_2 + \cdots + \frac{1}{n+1} {}_n \text{C}_n = \bm{\frac{1}{n+1}(2^{n+1}-1)} \end{align*}](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-34db7792c50c54d6902bf99b9d02c5a1_l3.png)
となる。
解説
二項定理
組み合わせの計算問題は頻出である。頻出であるが、気づかないと手が出ないものが多く、まさに経験がモノを言うタイプである。
ポイントは2つ、「二項定理を使うということに気づくこと」と「微分や積分でうまく係数を作り出すこと」である。
慣れも重要なので、過去に出題されたものを集めておく。一度経験することで、解き方のコツを頭に入れておくとよい。
類題
自然数 n に対して、次の等式が成り立つことを示せ。
(1) 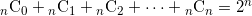
(2) 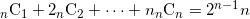
(3) 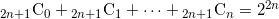 [2007 大阪府立大・理]
[2007 大阪府立大・理]
(1)
(2)
(3)
【解答】
(1) 上記の(1)と同じである。二項定理に x = 1 を代入して求められる。
(2) 実はこれが最も頻出の問題の一つ。二項定理の式を両辺 x で微分すると、
![]()
となり、これに x = 1 を代入すると、
![]()
となり示される。
(3) 二項定理の性質より、nCk = nCn-k が成り立つので、
![]()
である。ところで、
![]()
の値は、(1)で n を 2n + 1 として 22n+1であることから、求める値はこの半分の
![]()
となる。
(1)
(2)
(3)
この問題は、東京理科大の(3)のパターンで、積分が肝になっていると気付けば早い。(1)、(2)はいずれも変数に適切な数字を入れれば良いだけなので、まずは不定積分したものを計算して、あとで調整すると良い。(3)は(2)を利用します。
【解答】
二項定理の式を x で不定積分すると、
![]()
となる。ここで、 x = 0 とすると、![]() を得るので、
を得るので、
(*) ![]()
が成り立つ。
(1) (*)式に m = n , x = 1 を代入すれば、
![]()
より、
![]()
となる。
(2) (*)式に m = n , x = -1 を代入すれば、
![]()
となり、両辺を -1 で割って、
![]()
となる。
(3) (*)式に、 m = 2n , x = 1 とすると、
(**) ![Rendered by QuickLaTeX.com \[ \frac{1}{2n+1} \cdot 2^{2n+1} = \sum_{k=0}^{2n} \frac{1}{k+1} {}_{2n} \text{C}_k + \frac{1}{2n+1} \]](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-652ec78c6a1c1abb7abab7257b7eeeae_l3.png)
となる。つぎに、 m = 2n , x = -1 とすると、
(***) ![Rendered by QuickLaTeX.com \[ 0 = \sum_{k=0}^{2n} \frac{1}{k+1} {}_{2n} \text{C}_k (-1)^{k+1} + \frac{1}{2n+1} \]](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-6ae544d5ac2d6589587cf8de9e43852e_l3.png)
となる。(**)式-(***)式をして、
![]()
より、
![]()
となる。

コメント
2005年横市医学部の回答を教えてほしいです。
あと2007大阪府立に関しては、問題文も回答もなぜか表示されません。スマホで見てるからでしょうか
メッセージありがとうございました。
解答を公開しました。確認してみてください。
なお、2007大阪府大の問題の解答は公開しているのですが、数式がみられないということでしょうか?
もしかすると機種やソフトウェアによっては表示できないものがあるのかもしれません。
(すみません!すぐに対応できません。)
ありがとうございます。
横市は無事見れました!
前回見た時、大阪府立は横市の前に1つきちんとしたのがあり、後ろにももう一つこれは不完全な状態であったのですが、今見たところ後ろの方の大阪府立がなくなっていたので、おそらく前回見た時はなんらかのトラブルで横市の後に、大阪府立の問題が再び表示されてしまったのかも知れません。
お騒がせしました。