対数螺旋の性質［2000 神戸大・理（後）］

　a > 0 を定数として、座標平面上で次の式 x ( t ) = e^at cos t , y ( t ) = e^at sin t (-∞ < t < ∞) で定まる曲線を C_a とする。次の問いに答えよ。
(1)　位置ベクトル ( x ( t ) , y ( t ) ) と速度ベクトル ( x ‘ ( t ) , y ‘ ( t ) ) のなす角 θ は時刻 t によらず一定であることを示し、 θ と a の関係を求めよ。
(2)　 $\displaystyle \theta = \frac{\pi}{3}$ となる a に対し、曲線 C_a の 0 ≦ t ≦ 2π に対応する部分の長さを求めよ。

［2000 神戸大・理（後）］

イズミの解答への道

　対数螺旋とよばれる図形の性質に関する問題ですが、問題を解くだけであれば誘導に沿って計算を進めれば完答できるでしょう。

解答

(1)
x ‘ ( t ) = ae^at cos t – e^at sin t
　　　= e^at (a cos t – sin t)
y ‘ ( t ) = ae^at sin t + e^at cos t
　　　= e^at (a sin t + cos t)
である。求める角 θ は、

$\cos \theta = \frac{(x(t),y(t)) \cdot (x'(t),y'(t))}{|(x(t),y(t))||(x'(t),y'(t))|}$

で与えられるので、右辺の分母分子をそれぞれ求める。

　　( x ( t ) , y ( t ) )・( x ‘ ( t ) , y ‘ ( t ) )
　　　= e^2at { cos t ( a cos t – sin t ) + sin t ( cos t + a sin t ) }
　　　= e^2at × a = ae^2at

$\begin{align*} &| ( x ( t ) , y ( t ) ) | \\ &= e^{at} \sqrt{ \cos^2 t + \sin^2 t } = e^{at} \\ &| ( x ' ( t ) , y ' ( t ) ) | \\ &= e^{at} \sqrt{(a \cos t - \sin t )^2 +(a \sin t + \cos t )^2} \\ &= e^{at} \sqrt{a^2 + 1} \end{align*}$

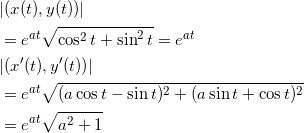
となるので、

$\cos \theta = \frac{ a e^{2at} }{e^{at} \cdot e^{at}\sqrt{a^2+1} } = \frac{a}{\sqrt{a^2 + 1}}$

となり、角 θ は時刻 t によらず一定であることを示す。

(2)　 $\displaystyle \theta = \frac{\pi}{3}$ のとき、(1)より、

$\frac{1}{2} = \frac{a}{\sqrt{a^2+1}}$

を解いて、 $\displaystyle a = \frac{1}{\sqrt{3}}$ である。このとき、求める長さ L は、

$\begin{align*} L &= \int_0^{2\pi} e^{at} \sqrt{a^2+1} dt \\ &=\sqrt{a^2+1} \int_0^{2\pi} e^{at} dt \\ &=\sqrt{a^2+1} \cdot \frac{1}{a} \left[ e^{at} \right]_0^{2\pi} \\ &=\frac{\sqrt{a^2+1}}{a} (e^{2\pi a} - 1 ) \end{align*}$

であり、ここに $\displaystyle a = \frac{1}{\sqrt{3}}$ を代入して、

$L = \bm{2 \left( e^{\frac{2\pi}{\sqrt{3}}} - 1 \right) }$

である。

対数螺旋の性質［2000 神戸大・理（後）］

イズミの解答への道

解答

解説

コメント