-1 < x < 1 の範囲で定義された関数 f ( x ) で、次の2つの条件を満たすものを考える。
![]() ( -1 < x < 1 , -1 < y < 1 )
( -1 < x < 1 , -1 < y < 1 )
f ( x ) は x = 0 で微分可能で、そこでの微分係数は 1 である
(1) -1 < x < 1 に対し f ( x ) = – f ( -x ) が成り立つことを示せ。
(2) f ( x ) は -1 < x < 1 の範囲で微分可能であることを示し、導関数 f ‘ ( x ) を求めよ。
(3) f ( x ) を求めよ。
[2015 東北大・理(後)]
イズミの解答への道
いわゆる関数方程式の問題。関数方程式の解法は、どこに気をつけなければいけないか、ということも含めてある程度決まっているので、過去問を解いて慣れておくことが重要である。
解答
(1)
![]()
において、 x = y = 0 とおくと、
2f ( 0 ) = f ( 0 )
より、 f ( 0 ) = 0 である。つぎに、 y = -x を代入すると、
f ( x ) + f ( -x ) = f( 0 ) = 0
となることより、
f ( x ) = – f ( -x )
であることが示された。
(2) -1 < x < 1 であるとき、 十分に小さい正の値 h を考えたとき、 x + h についても、 -1 < x + h < 1 である。
いま、
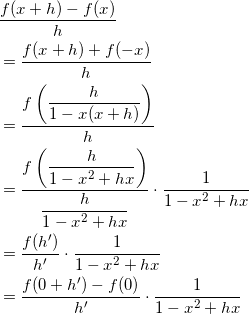
(ただし、![]() とおいた。)
とおいた。)
いま、 h → 0 のとき、 h’ → 0 であるから、
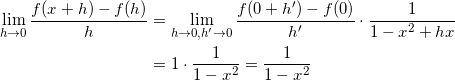
である。
これにより、 f ( x ) は -1 < x < 1 で微分可能であることが示され、 f ‘ ( x ) の値は、
![]()
である。
(3)
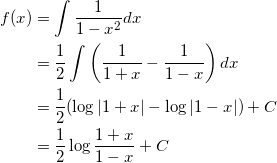
となり、f ( 0 ) = 0 だから、 C = 0 となるので、
![]()
解説
類題
関数方程式は類題が多いので、受験前にはどれも一度は経験しておくようにしたい。
- 関数方程式(指数関数) [2009 慈恵医大]?【類】2003杏林大・医
- 関数方程式(1次関数) [2005 静岡大・理・数]
- 関数方程式(tanh x) [2007 京都大・理乙]
- 関数方程式(sinh x , cosh x) [2008 東京医科歯科大]
- 関数方程式 [1989 東工大]

コメント