2020年センター数学IIB 第3問

問題

　数列 { a_n } は、初項 a₁ が 0 であり、 n = 1 , 2 , 3 , … のときに次の漸化式を満たすものとする。
　　a_n+1 = n + 3n + 1 { 3a_n + 3ⁿ⁺¹ – ( n + 1 )( n + 2 ) }……①

(1)　a₂ = 　ア　である。

(2)　b_n = a_n3ⁿ(n+1)(n+2) とおき、数列 { b_n } の一般項を求めよう。
　{ b_n } の初項 b₁ は　イ　である。①の両辺を 3ⁿ⁺¹( n + 2 )( n + 3 ) で割ると

　　b_n+1 = b_n + 　ウ　( n + 　エ　 ) ( n + 　オ　 ) – ( 1　カ　 )ⁿ⁺¹

を得る。ただし、　エ　 < 　オ　とする。
　したがって

　　b_n+1 – b_n = ( 　キ　n + 　エ　 – 　キ　n + 　オ　 ) – ( 1　カ　 )ⁿ⁺¹

である。

　n を2以上の自然数とするとき
　　 $\displaystyle \sum_{k=1}^{n-1}$ ( 　キ　n + 　エ　 – 　キ　n + 　オ　 ) = 1　ク　 ( n – 　ケ　n + 　コ　 )

　　 $\displaystyle \sum_{k=1}^{n-1}$ ( 1　カ　 )ⁿ⁺¹ = 　サ　　シ　 – 　ス　　セ　 ( 1　カ　 )ⁿ

が成り立つことを利用すると

　　b_n = n – 　ソ　　タ　 ( n + 　チ　 ) + 　ス　　セ　 ( 1　カ　 )ⁿ

が得られる。これは n = 1 のときも成り立つ。

(3)　(2)により、 { a_n } の一般項は
　
　　a_n = 　ツ　^n-テ ( n² – 　ト　 ) + ( n + 　ナ　 ) ( n + 　ニ　 )　ヌ　

で与えられる。ただし、　ナ　 < 　ニ　とする。
　このことから、すべての自然数 n について、 a_n は整数となることがわかる。

(4)　k を自然数とする。 a_3k , a_3k+1 , a_3k+2 を3で割った余りはそれぞれ　ネ　 , 　ノ　 , 　ハ　である。また、 { a_n } の初項から第2020項までの和を3で割った余りは　ヒ　である。

解答

アイ

　与えられた式に n = 1 を代入して、
　　a₂ = 42 { 3² – 2・3 } = 6

　同様に、n = 1 を代入すると、 a₁ = 0 なので、
　　b₁ = 0

ウエオカ

　問題文の指示通り、丁寧に割り算をすると、

$\begin{align*} b_{n+1} &= \frac{n+3}{n+1} 3a_n \cdot \frac{1}{3^{n+1}(n+2)(n+3)} \\ &\quad + \frac{n+3}{n+1} \frac{3^{n+1}}{3^{n+1}(n+2)(n+3)} \\ &\quad - \frac{n+3}{n+1} (n+1)(n+2) \cdot \frac{1}{3^{n+1}(n+2)(n+3)} \\ &=\frac{a_n}{3^n(n+1)(n+2)} + \frac{1}{(n+1)(n+2)} - \frac{1}{3^{n+1}} \\ &=b_n + \frac{1}{(n+\bm{1})(n+\bm{2})} - \left( \frac{1}{\bm{3}} \right)^{n+1} \end{align*}$

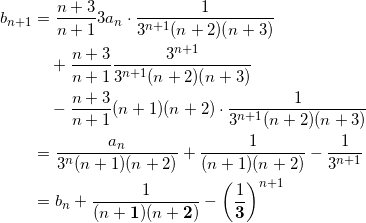
となる。

キ

　真ん中の項を部分分数分解して整理すると、

(※) $b_{n+1} - b_n = \left( \frac{1}{n+1} - \frac{1}{n+2} \right) - \left( \frac{1}{3} \right)^{n+1}$

となる。

クケコ

　定番の問題。書き下すとわかりやすいです。

$\begin{align*} &\sum_{k=1}^{n-1} \left( \frac{1}{k+1} - \frac{1}{k+2} \right) \\ &=\left( \frac{1}{2} - \frac{1}{3} \right) + \left( \frac{1}{3} - \frac{1}{4} \right) + \cdots + \left( \frac{1}{n} - \frac{1}{n+1} \right) \\ &=\frac{1}{2} - \frac{1}{n+1} \\ &=\frac{n+1-2}{2(n+1)} \\ &=\frac{1}{\bm{2}} \cdot \frac{n-\bm{1}}{n+\bm{1}} \end{align*}$

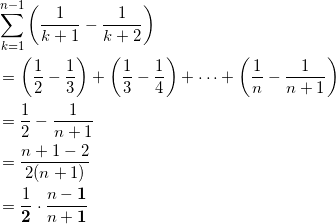
サシスセ

　こちらは等比数列の和の公式。初項1/9、公比1/3の等比数列の和（項数 n – 1 ）です。

$\begin{align*} &\sum_{k=1}^{n-1} \left( \frac{1}{3} \right)^{k+1} \\ &=\frac{\frac{1}{9} \left\{ 1- \left( \frac{1}{3} \right)^{n-1} \right\} }{1-\frac{1}{3}} \\ &=\frac{1}{6} \left\{ 1 - \left( \frac{1}{3} \right)^n-1 \right\} \\ &=\bm{\frac{1}{6}} - \bm{\frac{1}{2}} \left( \frac{1}{3} \right)^n \end{align*}$

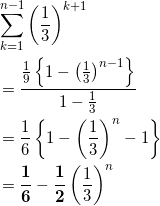
ソタチ

　これらの結果を利用して、(※)式を辺々足すと、

$\begin{align*} b_n - b_1 &= \frac{1}{2} \cdot \frac{n-1}{n+1} - \frac{1}{6} + \frac{1}{2} \cdot \left( \frac{1}{3} \right)^n \\ b_n &= \frac{3(n-1)-(n+1)}{6(n+1)} +\frac{1}{2} \cdot \left( \frac{1}{3} \right)^n \\ &=\frac{n-\bm{2}}{\bm{3}(n+\bm{1})} +\frac{1}{2} \cdot \left( \frac{1}{3} \right)^n \end{align*}$

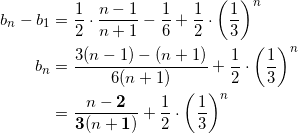
となる。

ツテトナニヌ

　改めて、

$\begin{align*} a_n &= \frac{n-2}{3(n+1)} \times 3^n (n+1)(n+2) \\ &\qquad + \frac{1}{2} \cdot \frac{1}{3^n} \times 3^n (n+1)(n+2) \\ &=\bm{3}^{n-\bm{1}} (n^2 - \bm{4} ) + \frac{(n+\bm{1})(n+\bm{2})}{\bm{2}} \end{align*}$

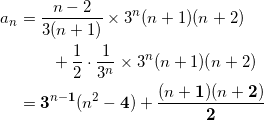
となる。（第2項は連続する2数は偶数なので、それを2で割った数も整数となる。）

ネノハ

　第1項は明らかに 3 の倍数（ n = 1 のときも、 1 – 4 = -3 より3の倍数となっている）なので、第2項を3で割ったあまりが幾つになるのかを確認する。
　　n = 3k のときは、3の倍数が含まれない。実際に見てみると、
　　　12(3k+1)(3k+2) = 9 × k(k+1)2 + 1 となり、余りは1である。
　　n = 3k + 1 , 3k + 2 のとき
　　　n + 1 , n + 2 のいずれかが3の倍数となることから、これらを3で割った余りは 0 となる。
よって、答えは順に、 1 , 0 , 0 である。

※マーク式の試験なので、
　・a₁ = 0 （3で割った余りは0）
　・a₂ = 6 （3で割った余りは0）
　・a₃ = 53 ( 18 + 27 – 12 ) = 55 （3で割った余りは1）
という事実だけから類推して解いてしまえばよい。そうすると、途中が解けなくてもここだけは正解できる。

ヒ

　3で割った余りに着目すると、
　　a₃ = 1 , a₆ = 1 , …
と3の倍数番目の項だけ余りが1になる。
　a₂₀₂₀ までに 3 の倍数は 673 回ある（2020 ÷ 3 = 673 あまり 1）ので、余りだけを足し合わせると673となる。最後にこれを3で割った余りが答えとなる。673 ÷ 3 = 224 あまり 1 となるので、答えは 1 となる。