難しい積分計算1 ［2002 芝浦工大］

$\displaystyle \tan \frac{\theta}{2} = x$ とおくとき、sinθ, cosθ を x で表すと、
　　　sinθ = 　　　 , cosθ = 　　　
であり、これらを利用すると、
　　 $\displaystyle \int_0^\frac{\pi}{2} \frac{d\theta}{1+\sin \theta + \cos \theta}$ = 　　　
である。

［2002 芝浦工大］

イズミの解答への道

　誘導通りに計算をしていけば答えは導かれます。とはいっても、 sinθ , cosθ を x で表す部分も、式変形に慣れていないと難しいかもしれません。

解答

　 $\displaystyle \tan \frac{\theta}{2} = x$ とおくと、 sinθ の2倍角の定理より、

$\begin{align*} &\sin \theta \\ &= 2 \sin \frac{\theta}{2} \cos \frac{\theta}{2} \end{align*}$

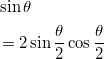
ここで、 sinθ = tanθ cosθ より、

$\begin{align*} =2 \tan \frac{\theta}{2} \cos^2 \frac{\theta}{2} \end{align*}$

であり、さらに $\displaystyle \cos^2 \theta = \frac{1}{1+ \tan^2 \theta}$ より、

$\begin{align*} =2 \tan \frac{\theta}{2} \cdot \frac{1}{\displaystyle 1 + \tan^2 \frac{\theta}{2}} =\bm{\frac{2x}{1+x^2}} \end{align*}$

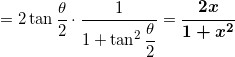
となる。また cosθ の2倍角の定理より、

$\begin{align*} \cos \theta &= 2 \cos^2 \frac{\theta}{2} - 1 = 2 \cdot \frac{1}{\displaystyle1+ \tan^2 \frac{\theta}{2}} -1 \\ &=\bm{\frac{1-x^2}{1+x^2}} \end{align*}$

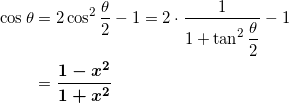
となる。
　つぎに $\displaystyle x = \tan \frac{\theta}{2}$ より、

$dx = \frac{d\theta}{\displaystyle 2 \cos^2 \frac{\theta}{2}} = \frac{d\theta}{2 \cdot \frac{1}{\displaystyle1+ \tan^2 \frac{\theta}{2}}} = \frac{1+x^2}{2} d\theta$

であるから、

$d\theta = \frac{2}{1+x^2} dx$

となる。また、積分範囲は、 $\displaystyle \theta : 0 \to \frac{\pi}{2}$ より、 $x : 0 \to 1$ なので、与えられた積分は、

$\begin{align*} \int_0^{\frac{\pi}{2}} \frac{d\theta}{1+\sin \theta + \cos \theta} &= \int_0^1 \frac{\displaystyle \frac{2}{1+x^2}}{\displaystyle 1 + \frac{2x}{1+x^2} + \frac{1-x^2}{1+x^2}} dx \\ &=\int_0^1 \frac{2}{1 + x^2 + 2x + 1 -x^2} dx \\ &=\int_0^1 \frac{1}{1+x} dx = [\log (1+x) ]_0^1 \\ &=\bm{\log 2} \end{align*}$

となる。

解説

∫ f (sinθ, cosθ) dθ

　この問題から、sinθ、cosθ（もちろん tanθ = sinθ/cosθ が含まれても良い）で構成される関数の積分は、tan θ/2 = x と置き換えれば、 x の関数に帰着できることが分かります。このことは高校の教科書では学ばないので、知らないと難しいでしょう。
　このような積分の常套手段は他にも多数あるので、一通り目を通しておきましょう。

以下は、作成中です

$\displaystyle \int \frac{1}{a^2 + x^2 } dx$
　特殊な積分計算2を参考ください。
$\displaystyle \int \frac{1}{\sqrt{x^2 +a^2}} dx$
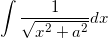
　特殊な積分計算3を参考ください。
∫ √(x^2 + a^2) dx
∫ √(a^2 – x^2) dx
∫ ex sin x dx
絶対値の入った積分
漸化式に持ち込む積分
さらにアイデアが必要な積分→旧赤チャp.200