問題
a > 0 とし、 f ( x ) = x2 – ( 4a – 2 ) x + 4a2 + 1 とおく。座標平面上で、放物線 y = x2 + 2x + 1 をC、放物線 y = f ( x ) を D とする。また、 l を C と D の両方に接する直線とする。
(1) lの方程式を求めよう。
lとCは点 ( t , t2 + 2t + 1 ) において接するとすると、 l の方程式は
y = ( ア t + イ ) x – t2 + ウ ……①
である。また、 l と D は点 ( s , f ( s ) ) において接するとすると、 l の方程式は
y = ( エ s – オ a + カ ) x – s2 + キ a2 + ク ……②
である。ここで、①と②は同じ直線を表しているので、 t = ケ , s = コ a が成り立つ。
したがって、 l の方程式は y = サ x + シ である。
(2) 二つの放物線 C , D の交点の x 座標は ス である。
Cと直線l , および直線 x = ス で囲まれた図形の面積を S とすると、 S = aセ ソ である。
(3) a ≧ 12 とする。二つの放物線 C , D と直線 l で囲まれた図形の中で 0 ≦ x ≦ 1 を満たす部分の面積 T は a > タ のとき、 a の値によらず
T = チ ツ
であり、 12 ≦ a ≦ タ のとき
T = – テ a3 + ト a2 – ナ a + ニ ヌ
である。
(4) 次に、(2)、(3)で定めた S , T に対して、 U = 2T – 3S とおく。 a が 12 ≦ a ≦ タ の範囲を動くとき、 U は a = ネ ノ で最大値 ハ ヒフ をとる。
解答
アイウ
接線の公式を用いて計算する。放物線 y = x2 + 2x + 1 について、
y’ = 2x + 2
であるから、x = t における接線は、
y = ( 2t + 2 ) ( x – t ) + t2 + 2t + 1
= ( 2t + 2 ) x – t2 + 1
である。
エオカキク
同様に、
f ‘ ( x ) = 2x – 4a + 2
であるから、放物線Dの x = s における接線は、
y = ( 2s – 4a + 2 ) ( x – s ) + s2 – ( 4a – 2 ) s + 4a2 + 1
= ( 2s – 4a + 2 ) x – s2 + 4a2 + 1
である。
ケコサシ
この2つの接線①、②が同じものを指していることから、係数を比較して、
2t + 2 = 2s – 4a + 2……①’
-t2 + 1 = -s2 +4a2 + 1……②’
となる。この連立方程式を解く。
①’より、 2a = s – t より、辺々2乗して
4a2 = ( s – t )2
を②’に代入して、
s2 – t2 = ( s – t )2
-2t2 + 2st = 0
となる。
ここで t ≠ 0 と仮定して両辺 t で割ると、
-t + s = 0 すなわち t = s となるが、このときは 2a = s – t = 0 となり不適。
よって、 t = 0 であり、このとき s = 2a となる。
これを①に代入して、接線 l の方程式は、
y = 2x + 1
となる。
ス
交点の座標は、連立方程式の解として求められるので、
x2 – ( 4a – 2 ) x + 4a2 + 1 = x2 + 2x + 1
4a2 – ( 4a – 2 ) x = 2x
a2 – ax = 0
a ≠ 0 であるから、
x – a = 0 すなわち x = a である。
セソ
面積を求めるときは簡単な図形を書いて考えること。
求める面積 S は、
![Rendered by QuickLaTeX.com \begin{align*} S &= \int_0^a \{ ( x^2+2x+1) - (2x+1) \}dx \\ &=\int_0^a x^2 dx \\ &=\left[ \frac{1}{3} x^3 \right]_0^a = \frac{a^\bm{3}}{\bm{3}} \end{align*}](https://izu-mix.com/math/wp-content/ql-cache/quicklatex.com-577b18e9a69f958d5b47ad4b6ee513fb_l3.png)
となる。
タチツ
積分範囲が、2つの放物線の交点より右か左かで、面積を求める式が変わることに着目する。
a < 1 のとき(すなわち a > 1 )、
![]()
である。
テトナニヌ
a ≦ 1 のとき、
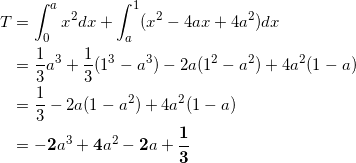
ネノハヒフ
最後は計算するだけです。
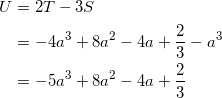
であるから、これを a で微分した
![]()
を解いて、![]() である。
である。
![]() であることから、最大値は a = 23 のときに取り、その値は、
であることから、最大値は a = 23 のときに取り、その値は、
![]()
である。

コメント